练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．要了解我县九年级学生的视力状况，从中抽查了1000名学生的视力状况，那么样本是指被抽查1000名学生的视力状况．

    分析 总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量．

    解答 解：了解我县九年级学生的视力状况，从中抽查了1000名学生的视力状况，那么样本是指被抽查1000名学生的视力状况，
    故答案为：被抽查1000名学生的视力状况．

    点评 考查了总体、个体、样本、样本容量，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目，不能带单位．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    15．因式分解：10am-15a=5a（2m-3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

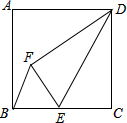    16．如图，在边长为12的正方形ABCD中，点E是边BC的中点，将△DCE沿DE折叠，点C落在正方形内的点F处，则△BEF的面积为$\frac{72}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

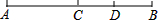    13．如图，C是线段AB的中点，D是线段CB的中点，下列说法错误的是（　　）
    A．CD=AC-BDB．CD=$\frac{1}{2}$AB-BDC．AC+BD=BC+CDD．CD=$\frac{1}{3}$AB

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

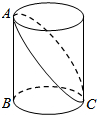    20．如图，已知圆柱底面的周长为4dm，圆柱高为2dm，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为4$\sqrt{2}$dm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．图1为长方形纸片ABCD，AD=26，AB=22，直线L、M皆为长方形的对称轴．今将长方形纸片沿着L对折后，再沿着M对折，并将对折后的纸片左上角剪下直角三角形，形成一个五边形EFGHI，如图2．最后将图2的五边形展开后形成一个八边形，如图2，且八边形的每一边长恰好均相等．
    （1）若图2中HI长度为x，请以x分别表示剪下的直角三角形的勾长和股长．
    （2）请求出图3中八边形的一边长的数值，并写出完整的解题过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．厦门市政府民生实事之一的公共自行车建设工作已基本完成，某部门对今年4月进行了公共日租车量的统计，估计4月份共租车2500000次，2500000用科学记数法表示为（　　）
    A．25×105B．2.5×106C．0.25×107D．2.5×107

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．
    （1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A=70°，∠B=80°．求∠C，∠D的度数．
    （2）在探究“等对角四边形”性质时：
    ①小红画了一个“等对角四边形”ABCD（如图2），其中∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立．请你证明此结论；
    ②由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等”．你认为她的猜想正确吗？若正确，请证明；若不正确，请举出反例．
    （3）已知：在“等对角四边形”ABCD中，∠DAB=60°，∠ABC=90°，AB=5，AD=4．求对角线AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：
    （1）操作发现：
    在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是①②③④（填序号即可）
    ①AF=AG=$\frac{1}{2}$AB；②MD=ME；③整个图形是轴对称图形；④MD⊥ME．
    （2）数学思考：
    在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD和ME具有怎样的数量关系和位置关系？请给出证明过程；
    （3）类比探索：
    在任意△ABC中，仍分别以AB、AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状．答：等腰直角三角形．

    查看答案和解析>>

    同步练习册答案