
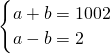 ,解得a=504,b=502,符号题意;
,解得a=504,b=502,符号题意;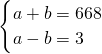 ,解得a=
,解得a=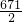 ,b=
,b=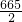 ,与正整数解矛盾,故舍去;
,与正整数解矛盾,故舍去;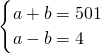 ,解得a=
,解得a=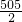 ,b=
,b=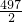 ,与正整数解矛盾,故舍去;
,与正整数解矛盾,故舍去;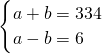 ,解得a=170,b=164,符号题意;
,解得a=170,b=164,符号题意;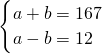 ,解得a=
,解得a= ,b=
,b=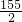 ,与正整数解矛盾,故舍去.
,与正整数解矛盾,故舍去.

科目:初中数学 来源: 题型:
|
|
|
|
|
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东威海市八年级下期末模拟数学试卷(二)(带解析) 题型:解答题
若正整数a、b、c满足方程a2+b2=c2 ,则称这一组正整数(a、b、c)为“商高数”,下面列举五组“商高数”:(3,4,5),(5,12,13),(6,8,10),(7,24,25),(12,16,20),注意这五组“商高数”的结构有如下规律: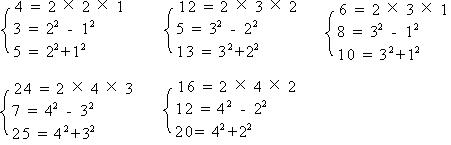
根据以上规律,回答以下问题:
(1)商高数的三个数中,有几个偶数,几个奇数?
(2)写出各数都大于30的两组商高数。
(3)用两个正整数m、n(m>n)表示一组商高数,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省威海市八年级下学期期末数学试卷(带解析) 题型:解答题
若正整数a、b、c满足方程a2+b2=c2 ,则称这一组正整数(a、b、c)为“商高数”,下面列举五组“商高数”:(3,4,5),(5,12,13),(6,8,10),(7,24,25),(12,16,20),注意这五组“商高数”的结构有如下规律: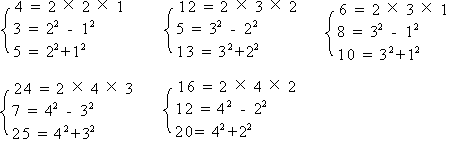
根据以上规律,回答以下问题:
(1) 商高数的三个数中,有几个偶数,几个奇数?
(2) 写出各数都大于30的两组商高数。
(3) 用两个正整数m、n(m>n)表示一组商高数,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省威海市八年级下学期期末数学试卷(解析版) 题型:解答题
若正整数a、b、c满足方程a2+b2=c2 ,则称这一组正整数(a、b、c)为“商高数”,下面列举五组“商高数”:(3,4,5),(5,12,13),(6,8,10),(7,24,25),(12,16,20),注意这五组“商高数”的结构有如下规律:
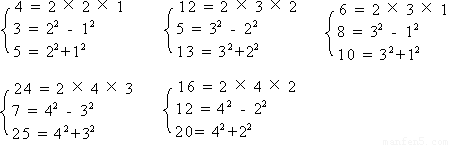
根据以上规律,回答以下问题:
(1) 商高数的三个数中,有几个偶数,几个奇数?
(2) 写出各数都大于30的两组商高数。
(3) 用两个正整数m、n(m>n)表示一组商高数,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源:2013届山东威海市八年级下期末模拟数学试卷(二)(解析版) 题型:解答题
若正整数a、b、c满足方程a2+b2=c2 ,则称这一组正整数(a、b、c)为“商高数”,下面列举五组“商高数”:(3,4,5),(5,12,13),(6,8,10),(7,24,25),(12,16,20),注意这五组“商高数”的结构有如下规律:
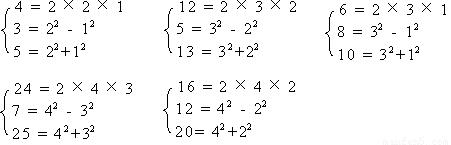
根据以上规律,回答以下问题:
(1)商高数的三个数中,有几个偶数,几个奇数?
(2)写出各数都大于30的两组商高数。
(3)用两个正整数m、n(m>n)表示一组商高数,并证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com