Question

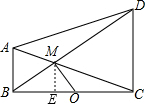
直角梯形ABCD中，AB∥CD，AB⊥BC，AC与BD交于M点，点O是BC中点，AB=2，CD=4，BC=6，则OM的长为

 

．

Answer 1

考点：相似三角形的判定与性质,勾股定理

专题：压轴题

分析：过点M作ME⊥BC于E，可以得出AB∥ME∥CD，就可以得出

AB

CD

=

AM

CM

=

BM

DM

=

1

2

，△BME∽△BDC，由相似三角形的性质就可以求出BE、ME的值，由勾股定理就可以求出OM的值．

解答：解：过点M作ME⊥BC于E，
∴∠MEB=∠MEC=90°．
∵AB⊥BC，
∴∠ABC=90°．
∴∠ABC=∠MEC，
∴AB∥ME．
∵AB∥CD，
∴AB∥ME∥CD．
∴△ABM∽△CDM，△BME∽△BDC，
∴

AB

CD

=

AM

CM

=

BM

DM

.

MB

MD

=

BE

CE

．
∵AB=2，CD=4，
∴

AB

CD

=

AM

CM

=

BM

DM

=

1

2

，
∴

BE

CE

=

BM

MD

，
∴

BE

CE

=

1

2

，
∴

BE

BC

=

1

3

，
∴

BE

6

=

1

3

，
即BE=2．
∵△BME∽△BDC，
∴

ME

CD

=

BE

BC

，
∴

ME

4

=

1

3

，
∴ME=

4

3

．
∵点O是BC中点，
∴BO=

1

2

BC=3．
∴EO=BO-BE=3-2=1．
在Rt△MEO中，由勾股定理，得
MO=

16 9 +1

=

5

3

．
故答案为：

5

3

．

点评：本题考查了平行线的性质的运用，相似三角形的判定与性质的运用，勾股定理的运用，线段中点的定义的运用，解答时证明三角形相似是解答本题的关键．