
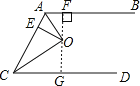
【题目】如图,AB∥CD,O为∠BAC,∠ACD平分线的交点,OE⊥AC交AC于E,AB与CD之间的距离等于4.8,OA=3,OC=4,求线段AC为(_______)

【答案】5
【解析】
过点O作FG⊥AB,交AB于点F,交CD于点G,则易得FG就是AB与CD之间的距离,再由O为∠BAC,∠ACD平分线的交点,可得OE=OF=OG,从而可得OE的长与∠AOC=90°,然后根据直角三角形的面积公式即可求出结果.
解:过点O作FG⊥AB,交AB于点F,交CD于点G,
∵AB∥CD,
∴FG⊥CD,∠BAC+∠ACD=180°,
∴FG就是AB与CD之间的距离.
∵O为∠BAC,∠ACD平分线的交点,OE⊥AC交AC于E,
∴OE=OF=OG,∠CAO=![]() ∠BAC,∠ACO=
∠BAC,∠ACO=![]() ∠ACD,
∠ACD,
∴2OE=4.8,即OE=2.4,∠CAO+∠ACO=![]() (∠ACD+∠BAC)=90°,即∠AOC=90°.
(∠ACD+∠BAC)=90°,即∠AOC=90°.
根据三角形的面积可得:![]() ,即
,即![]() ,解得AC=5.
,解得AC=5.
故答案为:5.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商经销的学生用品,他以每件280元的价格购进某种型号的学习机,以每件360元的售价销售时,每月可售出60个,为了扩大销售,该经销商采取降价的方式促销,在销售中发现,如果每个学习机降价1元,那么每月就可以多售出5个.
![]() 降价前销售这种学习机每月的利润是多少元?
降价前销售这种学习机每月的利润是多少元?
![]() 经销商销售这种学习机每月的利润要达到7200元,且尽可能让利于顾客,求每个学习机应降价多少元?
经销商销售这种学习机每月的利润要达到7200元,且尽可能让利于顾客,求每个学习机应降价多少元?
![]() 在
在![]() 的销售中,销量可好,经销商又开始涨价,涨价后每月销售这种学习机的利润能达到10580元吗?若能,请求出涨多少元;若不能,请说明理由.
的销售中,销量可好,经销商又开始涨价,涨价后每月销售这种学习机的利润能达到10580元吗?若能,请求出涨多少元;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=5:2,则∠AOF等于( )

A. 140° B. 130° C. 120° D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
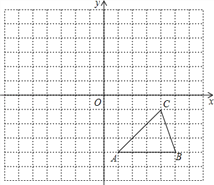
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D是AC边上一动点,CE⊥BD于E.

(1)如图(1),若BD平分∠ABC时,①求∠ECD的度数;②延长CE交BA的延长线于点F,补全图形,探究BD与EC的数量关系,并证明你的结论;
(2)如图(2),过点A作AF⊥BE于点F,猜想线段BE,CE,AF之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019 年 3 月 31 日,南京地铁新的价格方案正式实施,实行消费累进优惠.普通成人每月持卡乘坐地铁,当消费累计金额不超过 150 元时,每次乘坐地铁的票价打 9.5 折;当消费累计金 额超过 150 元时,达到规定的消费累计金额后的乘次,票价所打折扣如下表所示:
消费累计金额 | 折扣 |
| 9折 |
| 8折 |
| 9.5折 |
小明上、下班每次乘坐的地铁单程票价为 10元,2019年 4月份他上、下班持卡共乘坐了 40次.
(1)填表:
第1 次 | 第2 次 | … | 第15次 | 第16次 | 第17次 | … | |
消费累计 金额(元) | 9.5 | 19 | … | 142.5 | 152 | … |
span>
(2)小明当月第几次乘车后,消费累计金额超过 20元?(用一元一次不等式解决问题)
(3)小明 4月份上、下班持卡乘坐地铁的消费累计金额为 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com