
(本题9分)两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1. 固定△ABC不动,将△DEF进行如下操作:
(1)如图1,△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.
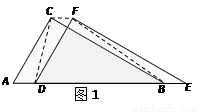
(2)如图2,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
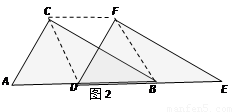
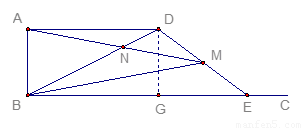
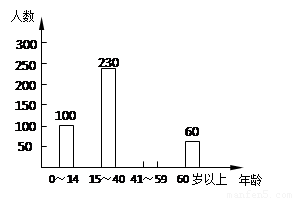 (3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinAED的值.
(3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinAED的值.
(1)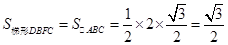 ;(2)四边形CDBF是菱形;
;(2)四边形CDBF是菱形;
(3) sinα=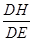 =
=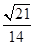 。
。
【解析】此题主要考查了菱形的判定,综合运用直角三角形的性质和平移的性质进行分析计算,考查学生综合运用数学知识的能力.
(1)过点C作CG⊥AB于G
在Rt△ACG中 ∵∠A=60°
∴sin60°=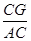 ,得到结论。
,得到结论。
(2)根据直角三角形斜边上的中线等于斜边的一半和平移的性质,即可得到该四边形的四条边都相等,则它是一个菱形;
(3)在Rt△ABE中 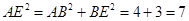
∴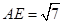 过点D作DH⊥AE 垂足为H
过点D作DH⊥AE 垂足为H
则△ADH∽△AEB 得到相似比求解得到。
(1)过点C作CG⊥AB于G
在Rt△ACG中 ∵∠A=60°
∴sin60°=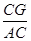 ∴
∴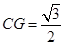 ……………1分
……………1分
在Rt△ABC中 ∠ACB=90°∠ABC=30°
∴AB=2 …………………………………………2分
∴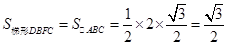 ………3分
………3分
(2)菱形………………………………………4分
∵D是AB的中点 ∴AD=DB=CF=1
在Rt△ABC中,CD是斜边中线 ∴CD=1……5分
同理 BF=1 ∴CD=DB=BF=CF
∴四边形CDBF是菱形…………………………6分
(3)在Rt△ABE中 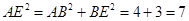
∴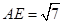 ……………………………7分
……………………………7分
过点D作DH⊥AE 垂足为H
则△ADH∽△AEB ∴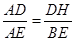
即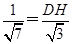 ∴ DH=
∴ DH=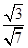 ……8分
……8分
在Rt△DHE中
sinα=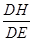 =…=
=…=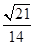 …………………9分
…………………9分



 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
(本题满分8分)两个全等的直角三角形重叠放在直线![]() 上,如图⑴,AB=6
上,如图⑴,AB=6![]() ,BC=8
,BC=8![]() ,∠ABC=90°,将Rt△ABC在直线
,∠ABC=90°,将Rt△ABC在直线![]() 上左右平移,如图⑵所示.
上左右平移,如图⑵所示.
⑴ 求证:四边形ACFD是平行四边形;
⑵ 怎样移动Rt△ABC,使得四边形ACFD为菱形;
⑶ 将Rt△ABC向左平移![]() ,求四边形DHCF的面积.
,求四边形DHCF的面积.

查看答案和解析>>
科目:初中数学 来源:四川省凉山州2011年中考数学试题 题型:解答题
(本题满分8分)两个全等的直角三角形重叠放在直线 上,如图⑴,AB=6
上,如图⑴,AB=6 ,BC=8
,BC=8 ,∠ABC=90°,将Rt△ABC在直线
,∠ABC=90°,将Rt△ABC在直线 上左右平移,如图⑵所示.
上左右平移,如图⑵所示.
⑴求证:四边形ACFD是平行四边形;
⑵怎样移动Rt△ABC,使得四边形ACFD为菱形;
⑶将Rt△ABC向左平移 ,求四边形DHCF的面积.
,求四边形DHCF的面积.
查看答案和解析>>
科目:初中数学 来源:2012届山东省淄博市桓台县毕业班复习质量质量检测数学试卷(带解析) 题型:解答题
(本题9分)两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC="1." 固定△ABC不动,将△DEF进行如下操作:
(1)如图1,△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.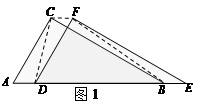
(2)如图2,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.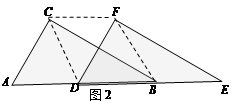
 (3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinAED的值.
(3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinAED的值.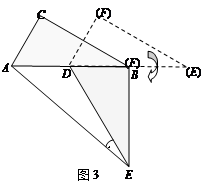
查看答案和解析>>
科目:初中数学 来源:四川省凉山州2011年中考数学试题 题型:解答题
(本题满分8分)两个全等的直角三角形重叠放在直线 上,如图⑴,AB=6
上,如图⑴,AB=6 ,BC=8
,BC=8 ,∠ABC=90°,将Rt△ABC在直线
,∠ABC=90°,将Rt△ABC在直线 上左右平移,如图⑵所示.
上左右平移,如图⑵所示.
⑴ 求证:四边形ACFD是平行四边形;
⑵ 怎样移动Rt△ABC,使得四边形ACFD为菱形;
⑶ 将Rt△ABC向左平移 ,求四边形DHCF的面积.
,求四边形DHCF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com