Question

4．（1）如图（1），直线a∥b，A，B两点分别在直线a，b上，点P在a，b外部，则∠1，∠2，∠3之间有何数量关系？证明你的结论；
（2）如图（2），直线a∥b，点P在直线a，b直角，∠2=50°，∠3=30°，求∠1；
（3）在图（2）中，将直线a绕点A按逆时针方向旋转一定角度交直线b于点M，如图（3），若∠1=100°，∠4=40°，求∠2+∠3的度数．

Answer 1

分析 （1）设直线AP交直线b于O，根据平行线的性质得出∠2=∠AOB，根据三角形外角性质求出∠AOB=∠1+∠3，即可得出答案；
（2）延长AP交直线b于O，根据平行线的性质得出∠ABO=∠2=50°，根据三角形的外角性质得出∠1=∠AOB+∠3，代入求出即可；
（3）延长AP交直线b于O，根据三角形外角性质得出∠AOB=∠2+∠4，∠1=∠3+∠AOB，求出∠1=∠2+∠4+∠3，代入求出即可．

解答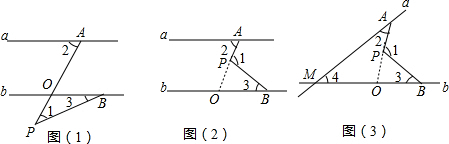
（1）∠2=∠1+∠3，
证明：设直线AP交直线b于O，如图1，
∵直线a∥直线b，
∴∠2=∠AOB，
∵∠AOB=∠1+∠3，
∴∠2=∠1+∠3；

（2）解：延长AP交直线b于O，如图2，
∵直线a∥直线b，∠2=50°，
∴∠ABO=∠2=50°，
∵∠3=30°，
∴∠1=∠AOB+∠3=50°+30°=80°；

（3）解：延长AP交直线b于O，如图3，
∵∠AOB=∠2+∠4，∠1=∠3+∠AOB，
∴∠1=∠2+∠4+∠3，
∵∠1=100°，∠4=40°，
∴∠2+∠3=∠1-∠4=60°．

点评 本题考查了平行线的性质，三角形外角性质的应用，能灵活运用性质进行推理是解此题的关键．