
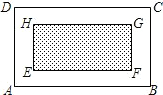
 如图,某居民小区,有矩形地ABCD一块,为美化环境要在中央修建一矩形EFGH花圃,使其面积为这块地面积的一半,且花圃四周的道路宽相等,今无测量工具,只有无刻度的足够长的一条绳子,如何量出道路的宽度?
如图,某居民小区,有矩形地ABCD一块,为美化环境要在中央修建一矩形EFGH花圃,使其面积为这块地面积的一半,且花圃四周的道路宽相等,今无测量工具,只有无刻度的足够长的一条绳子,如何量出道路的宽度? 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
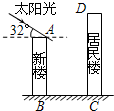 某居民小区有一朝向为正南方向的居民楼(如图 ),该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为32°时.
某居民小区有一朝向为正南方向的居民楼(如图 ),该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为32°时.| 53 |
| 100 |
| 106 |
| 125 |
| 5 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
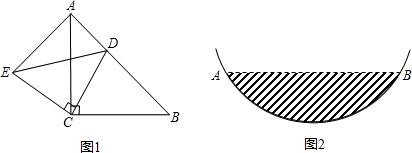
 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,则这个圆形截面的半径为
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,则这个圆形截面的半径为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com