
 在一场篮比赛中,甲球员在距篮4米处跳投,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.75米,然后球准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
在一场篮比赛中,甲球员在距篮4米处跳投,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.75米,然后球准确落入篮圈.已知篮圈中心到地面的距离为3.05米. ,
, x2+3.75(-2.5≤x≤1.5);
x2+3.75(-2.5≤x≤1.5); ×(-0.5)2+3.75≈3.69,
×(-0.5)2+3.75≈3.69, x2+3.75=3.15,
x2+3.75=3.15,

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
 某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高| 20 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
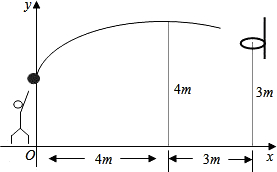 离地面
离地面| 20 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高| 20 | 9 |
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题
 m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com