
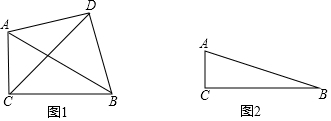
分析 (1)先判断出∠CAD=∠DBE,再利用等腰直角三角形求出∠ABD=45°,进而求出∠CBD,最后用邻补角即可得出结论;
(2)①根据题意及基本作图即可补全图形;
②想法1,构造出△ACD≌△BED,进而判断出△CDE是等腰直角三角形,再利用等腰直角三角形的性质即可得出解;
想法2,构造出△BDH≌△ADG,进而判断出△CDH是等腰直角三角形,再利用等腰直角三角形的性质即可得出结论;
(3)同(2)的方法即可得出结论.
解答 解:(1)∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵△ADB是等腰直角三角形,
∴∠ABD=45°,
∵∠ABC=30°,
∴∠CBD=∠ABD+∠ABC=75°,
∴∠CAD=∠DBE=180°-75°=105°
故答案为:105°.
(2)①补全图形,如图1所示.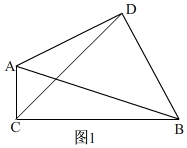
②想法1:
如图2,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.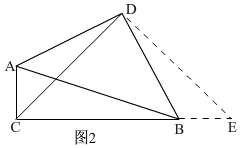
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∵AC=1,BC=3,
∴CE=4.
∴CD=$2\sqrt{2}$.
想法2:如图2,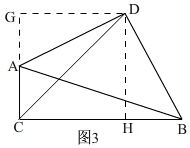
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DAG+∠CAD═180°,
∴∠CBD=∠DAG.
∵DA=DB,∠DGA=∠DHB=90°,
∴△BDH≌△ADG.
∴DH=DG,BH=AG.
∴∠DCH=∠DCG=45°.
∴△CHD为等腰直角三角形.
∵AC=1,BC=3,
∴CH=2.
∴CD=$2\sqrt{2}$.
(3)AC+BC=$\sqrt{2}$CD,
理由:如图2,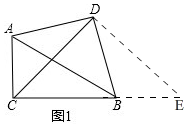
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD═180°.
∵∠DBE+∠CBD═180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∴CE=$\sqrt{2}$CD,
∵CE=BC+BE=BC+AC.
即:$AC+BC=\sqrt{2}CD$.
点评 此题是三角形综合题,主要考查了等角的补角相等,全等三角形的判定和性质,等腰直角三角形的性质和判定,解本题的关键是构造出全等三角形,进而判断出△CDE或△CDH是等腰直角三角形,是一道中等难度的中考常考题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
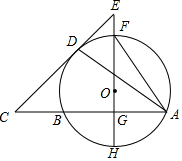 已知,FH是⊙O的直径,弦AB⊥FH于G,过AB的延长线上一点C作⊙O的切线交HF于E,切点为点D,连接AF、AD.
已知,FH是⊙O的直径,弦AB⊥FH于G,过AB的延长线上一点C作⊙O的切线交HF于E,切点为点D,连接AF、AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
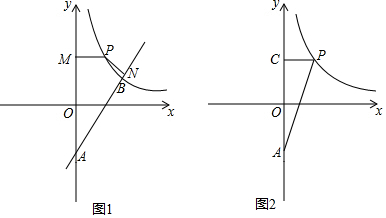
 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为( )
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
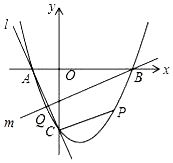 抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,-3)
抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,-3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com