
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
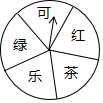 某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶、红茶和可乐.
某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶、红茶和可乐.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12×105 | B. | 1.2×106 | C. | 1.2×105 | D. | 0.12×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 22.3×103 | B. | 2.23×104 | C. | 0.223×105 | D. | 2.23×100 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
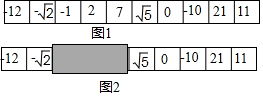 如图1,一张纸条上依次写有10个数,如图2,一卡片每次可以盖住纸条上的3个数,那么随机地用卡片盖住的3个数中有且只有一个是负数的概率$\frac{1}{2}$.
如图1,一张纸条上依次写有10个数,如图2,一卡片每次可以盖住纸条上的3个数,那么随机地用卡片盖住的3个数中有且只有一个是负数的概率$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.38×104元 | B. | 73.8×105元 | C. | 7.38×106元 | D. | 0.738×106元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com