
已知:如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边AB相交于点E,且AE=3EB.
(1)求证:△ADE∽△CDF;
(2)当CF:FB=1:2时,求⊙O与▱ABCD的面积之比.
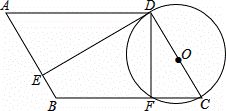
(1)证明 :∵CD是⊙O的直径,
:∵CD是⊙O的直径,
∴∠DFC=90°,
∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,
∴∠ADF=∠DFC=90°,
∵DE为⊙O的切线,
∴DE⊥DC,
∴∠EDC=90°,
∴∠ADF=∠EDC=90°,
∴∠ADE=∠CDF,
∵∠A=∠C,
∴△ADE∽△CDE;
(2)解:∵CF:FB=1:2,
∴设CF=x,FB=2x,则BC=3x,
∵AE=3EB,
∴设EB=y,则AE=3y,AB=4y,
∵四边形ABCD是平行四边形,
∴AD=BC=3x,AB=DC=4y,
∵△ADE∽△CDF,
∴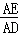 =
=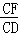 ,
,
∴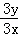 =
= ,
,
∵x、y均为正数,
∴x=2y,
∴BC=6y,CF=2y,
在Rt△DFC中,∠DFC=90°,
由勾股定理得:DF=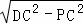 =
=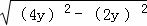 =2
=2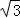 y,
y,
∴⊙O的面积为π•( DC)2=
DC)2=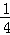 π•DC2=
π•DC2=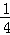 π(4y)2=4πy2,
π(4y)2=4πy2,
四边形ABCD的面积为BC•DF=6y•2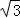 y=12
y=12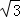 y2,
y2,
∴⊙O与四边形ABCD的面积之比为4πy2:12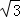 y2=π:3
y2=π:3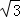 .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
甲、乙、丙三位同学进行报数游戏,游戏规则为:甲报1,乙报2,丙报3,再甲报4,乙报5,丙报6,…依次循环反复下去,当报出的数为2014时游戏结束,若报出的数是偶数,则该同学得1分.当报数结束时甲同学的得分是 分.
查看答案和解析>>
科目:初中数学 来源: 题型:
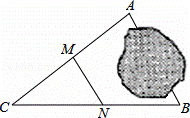
如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
|
| A. | AB=24m | B. | MN∥AB | C. | △CMN∽△CAB | D. | CM:MA=1:2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
为促进义务教育办学条件均衡,某市投入480万元资金为部分学校添置实验仪器及音、体、美器材,480万元用科学记数法表示为( )
| A. | 480×104元 | B. | 48×105元 | C. | 4.8×106元 | D. | 0.48×107元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com