
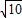 ,tan∠ABO=3,直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以
,tan∠ABO=3,直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以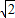 个单位每秒速度运动,运动时间为t,求:
个单位每秒速度运动,运动时间为t,求: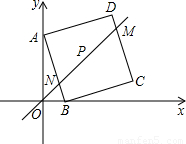
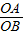 =3,设OA=3x,则OB=x,再根据正方形ABCD的边长为
=3,设OA=3x,则OB=x,再根据正方形ABCD的边长为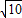 利用勾股定理可求出OA及OB的长,由全等三角形的判定定理可得出△AOB≌△BEC≌△DFA,故可得出CD的坐标,利用中点坐标公式即可得出P点坐标;
利用勾股定理可求出OA及OB的长,由全等三角形的判定定理可得出△AOB≌△BEC≌△DFA,故可得出CD的坐标,利用中点坐标公式即可得出P点坐标;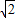 ,H速度为1,且∠ROH=45°,可知tan∠ROH=1,故RH始终垂直于x轴,RH=OH=t,设△HCR的边RH的高为h,h=|4-t|,再由三角形的面积公式即可得出结论;
,H速度为1,且∠ROH=45°,可知tan∠ROH=1,故RH始终垂直于x轴,RH=OH=t,设△HCR的边RH的高为h,h=|4-t|,再由三角形的面积公式即可得出结论;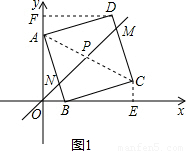 解:(1)如图1,过点D作DF⊥y轴于点F,作CE⊥x轴于点E,连接AC,
解:(1)如图1,过点D作DF⊥y轴于点F,作CE⊥x轴于点E,连接AC, =3,
=3,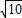 ,
,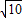 )2,
)2,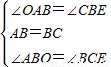 ,
,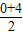 ,
,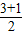 ),即(2,2),
),即(2,2),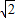 ,H速度为1,且∠ROH=45°,
,H速度为1,且∠ROH=45°, =|-t2+4t|•
=|-t2+4t|• ,
, t2+2t(0<t<4)或S=
t2+2t(0<t<4)或S= t2-2t(t>4);
t2-2t(t>4); t2+2t(0<t≤4)或S=
t2+2t(0<t≤4)或S= t2-2t(t>4);
t2-2t(t>4);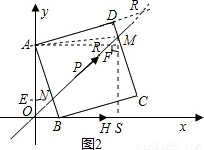
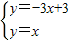 ,
,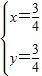 ,
,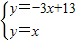 ,
,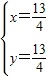
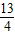 ,
,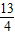 ),
),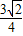 ,OM=
,OM=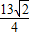 ,
,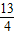 )2+(
)2+( )2,
)2,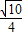 ,AN=
,AN=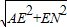 =
=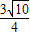 ,
,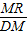 =
=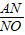 ,即
,即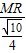 =
= ,
, ,
, ,
,
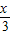 +3.
+3.
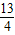 ,
,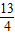 )
)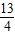 ,
, ,
, )求出t=
)求出t= .
.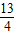 或t=
或t= .
.

 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.查看答案和解析>>
科目:初中数学 来源: 题型:
 OM方向以
OM方向以| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
 向以
向以| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 10 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com