
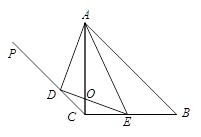
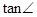 BAE = y,求y关于x的函数解析式,并写出它的定义域;
BAE = y,求y关于x的函数解析式,并写出它的定义域;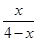 ,定义域0<x<2;(3)当CD=
,定义域0<x<2;(3)当CD=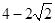 时,△COD与△BEA相似.
时,△COD与△BEA相似.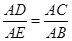
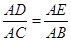 且∠DAE=∠CAB=45°
且∠DAE=∠CAB=45°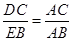
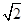 x
x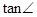 BAE=
BAE=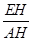
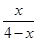
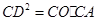
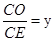
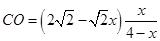
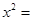
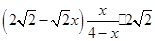
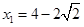 ,
,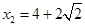
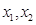 都是原方程的实数根,
都是原方程的实数根,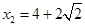 不合题意舍去
不合题意舍去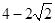 时,△COD与△BEA相似.
时,△COD与△BEA相似.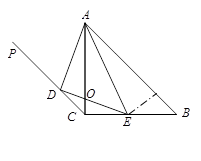


科目:初中数学 来源:不详 题型:解答题
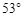 ,则秋千踏板与地面的最大距离约为多少?(参考数据:
,则秋千踏板与地面的最大距离约为多少?(参考数据: ≈0.8,
≈0.8, 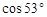 ≈0.6)
≈0.6)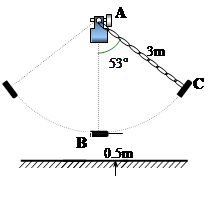
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ≈1.73)
≈1.73)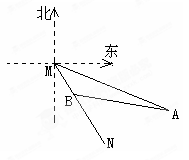
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com