
ΓΨΧβΡΩΓΩ»γΆΦΘ§RtΓςABOΒΡΝΫ÷±Ϋ«±ΏOAΓΔOBΖ÷±π‘Ύx÷αΒΡΗΚΑκ÷αΚΆy÷αΒΡ’ΐΑκ÷α…œΘ§OΈΣΉχ±ξ‘≠ΒψΘ§AΓΔBΝΫΒψΒΡΉχ±ξΖ÷±πΈΣΘ®![]() Θ§0Θ©ΓΔΘ®0Θ§4Θ©Θ§≈ΉΈοœΏ
Θ§0Θ©ΓΔΘ®0Θ§4Θ©Θ§≈ΉΈοœΏ![]() Ψ≠ΙΐBΒψΘ§«“ΕΞΒψ‘Ύ÷±œΏ
Ψ≠ΙΐBΒψΘ§«“ΕΞΒψ‘Ύ÷±œΏ![]() …œΘ°
…œΘ°
Θ®1Θ©«σ≈ΉΈοœΏΕ‘”ΠΒΡΚ· ΐΙΊœΒ ΫΘΜ
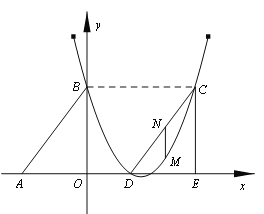
Θ®2Θ©»τΓςDCE «”…ΓςABO―Ίx÷αœρ”“ΤΫ“ΤΒΟΒΫΒΡΘ§Β±ΥΡ±Ώ–ΈABCD «Νβ–Έ ±Θ§ ‘≈–ΕœΒψCΚΆΒψD «Ζώ‘ΎΗΟ≈ΉΈοœΏ…œΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®3Θ©»τMΒψ «CDΥυ‘Ύ÷±œΏœ¬ΖΫΗΟ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψMΉςMNΤΫ––”Ύy÷αΫΜCD”ΎΒψNΘ°…ηΒψMΒΡΚαΉχ±ξΈΣtΘ§MNΒΡ≥ΛΕ»ΈΣlΘ°«σl”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σl»ΓΉν¥σ÷Β ±Θ§ΒψMΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]()
Θ®2Θ©‘ΎΘ§άμ”…¬‘
Θ®3Θ©MΒΡΉχ±ξΈΣΘ®![]() Θ§
Θ§ ![]() Θ©
Θ©
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©“―÷ΣΝΥ≈ΉΈοœΏ…œAΓΔBΒψΒΡΉχ±ξ“‘ΦΑ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΖΫ≥ΧΘ§Ω…”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘ°
Θ®2Θ© Ήœ»«σ≥ωABΒΡ≥ΛΘ§ΫΪAΓΔBΒΡΉχ±ξœρ”“ΤΫ“ΤABΗωΒΞΈΜΘ§Φ¥Ω…ΒΟ≥ωCΓΔDΒΡΉχ±ξΘ§‘Ό¥ζ»κ≈ΉΈοœΏΒΡΫβΈω Ϋ÷–Ϋχ––―ι÷ΛΦ¥Ω…Θ°
Θ®3Θ©ΗυΨίCΓΔDΒΡΉχ±ξΘ§“Ή«σΒΟ÷±œΏCDΒΡΫβΈω ΫΘΜΡ«Ο¥œΏΕΈMNΒΡ≥Λ ΒΦ «÷±œΏBC”κ≈ΉΈοœΏΒΡΚ· ΐ÷ΒΒΡ≤νΘ§Ω…ΫΪx=t¥ζ»κΝΫΗωΚ· ΐΒΡΫβΈω Ϋ÷–Θ§ΒΟ≥ωΒΡΝΫΚ· ΐ÷ΒΒΡ≤νΦ¥ΈΣlΒΡ±μ¥ο ΫΘ§”…¥ΥΩ…«σ≥ωlΓΔtΒΡΚ· ΐΙΊœΒ ΫΘ§ΗυΨίΥυΒΟΚ· ΐΒΡ–‘÷ Φ¥Ω…«σ≥ωl»ΓΉν¥σ÷Β ±Θ§ΒψMΒΡΉχ±ξΘ°
ΫβΘΚΘ®1Θ©ΓΏ≈ΉΈοœΏy=![]() +bx+cΒΡΕΞΒψ‘Ύ÷±œΏx=…œΘ§
+bx+cΒΡΕΞΒψ‘Ύ÷±œΏx=…œΘ§
ΓύΩ……ηΥυ«σ≈ΉΈοœΏΕ‘”ΠΒΡΚ· ΐΙΊœΒ ΫΈΣy=![]() +m
+m
ΓΏΒψBΘ®0Θ§4Θ©‘Ύ¥Υ≈ΉΈοœΏ…œΘ§
Γύ4=ΓΝ![]() +m
+m
Γύm=©¹
ΓύΥυ«σΚ· ΐΙΊœΒ ΫΈΣΘΚy=![]() ©¹=
©¹=![]() ©¹
©¹![]() x+4
x+4
Θ®2Θ©‘ΎRtΓςABO÷–Θ§OA=3Θ§OB=4Θ§
ΓύAB=![]() =5
=5
ΓΏΥΡ±Ώ–ΈABCD «Νβ–Έ
ΓύBC=CD=DA=AB=5
ΓύCΓΔDΝΫΒψΒΡΉχ±ξΖ÷±π «Θ®5Θ§4Θ©ΓΔΘ®2Θ§0Θ©ΘΜ
Β±x=5 ±Θ§y=ΓΝ52©¹![]() ΓΝ5+4=4
ΓΝ5+4=4
Β±x=2 ±Θ§y=ΓΝ22©¹![]() ΓΝ2+4=0
ΓΝ2+4=0
ΓύΒψCΚΆΒψD‘ΎΥυ«σ≈ΉΈοœΏ…œΘΜ
Θ®3Θ©…η÷±œΏCDΕ‘”ΠΒΡΚ· ΐΙΊœΒ ΫΈΣy=kx+bΓδΘ§
‘ρ![]() ΘΜ
ΘΜ
ΫβΒΟΘΚ![]() ΘΜ
ΘΜ
Γύy=x©¹
ΓΏMNΓΈy÷αΘ§MΒψΒΡΚαΉχ±ξΈΣtΘ§
ΓύNΒψΒΡΚαΉχ±ξ“≤ΈΣtΘΜ
‘ρyM=![]() ©¹
©¹![]() t+4Θ§yN=t©¹Θ§
t+4Θ§yN=t©¹Θ§
Γύl=yN©¹yM=t©¹©¹Θ®![]() ©¹
©¹![]() t+4Θ©=©¹
t+4Θ©=©¹![]() +
+![]() t©¹
t©¹![]() =©¹
=©¹![]() +
+
ΓΏ©¹ΘΦ0Θ§
ΓύΒ±t= ±Θ§lΉν¥σ=Θ§yM=![]() ©¹
©¹![]() t+4=Θ°
t+4=Θ°
¥Υ ±ΒψMΒΡΉχ±ξΈΣΘ®Θ§Θ©Θ°


 ΩΎΥψΡή ÷œΒΝ–¥πΑΗ
ΩΎΥψΡή ÷œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§PΓΔQΖ÷±π «BCΓΔAC…œΒΡΒψΘ§ΉςPRΓΆABΘ§PSΓΆACΘ§¥ΙΉψΖ÷±πΈΣRΓΔSΘ§»τAQ=PQΘ§PR=PSΘ§‘ρœ¬Ν–ΥΡΗωΫα¬έΘΚΔΌPAΤΫΖ÷ΓœBACΘΜΔΎAS=ARΘΜΔέQPΓΈARΘΜΔήΓςBRPΓ’ΓςCSPΘ§Τδ÷–Ϋα¬έ’ΐ»ΖΒΡ–ρΚ≈ΈΣΘ® Θ© 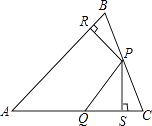
A.ΔΌΔΎΔέ
B.ΔΌΔΎΔή
C.ΔΎΔέΔή
D.ΔΌΔΎΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΑ―œ¬Ν–Ης ΐΧν‘Ύœύ”ΠΒΡά®Κ≈άοΘΚ
©¹8Θ§0.275Θ§ ![]() Θ§0Θ§©¹1.04Θ§©¹Θ®©¹3Θ©Θ§©¹
Θ§0Θ§©¹1.04Θ§©¹Θ®©¹3Θ©Θ§©¹ ![]() Θ§|©¹2|
Θ§|©¹2|
’ΐ ΐΦ·Κœ{Γ≠}
ΗΚ’ϊ ΐΦ·Κœ{Γ≠}
Ζ÷ ΐΦ·Κœ{Γ≠}
ΗΚ ΐΦ·Κœ{Γ≠}Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν– ΫΉ”÷–Θ§≤ΜΡή≥…ΝΔΒΡ «Θ® Θ©
A.©¹Θ®©¹2Θ©=2
B.©¹|©¹2|=©¹2
C.23=6
D.Θ®©¹2Θ©2=4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΦΰ”π»όΖΰœ»Α¥≥…±ΨΧαΗΏ50%±ξΦέΘ§‘Ό“‘8’έΘ®±ξΦέΒΡ80%Θ©≥ω έΘ§ΫαΙϊΜώάϊ250‘ΣΘ°»τ…η’βΦΰ”π»όΖΰΒΡ≥…±Ψ «x‘ΣΘ§ΗυΨίΧβ“βΘ§Ω…ΒΟΒΫΒΡΖΫ≥Χ «Θ® Θ©
A.xΘ®1+50%Θ©ΓΝ80%=x©¹250
B.xΘ®1+50%Θ©ΓΝ80%=x+250
C.Θ®1+50%xΘ©ΓΝ80%=x©¹250
D.Θ®1+50%xΘ©ΓΝ80%=250©¹x
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
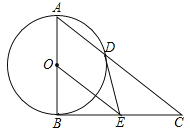
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœABCΘΫ90ΓψΘ§“‘ABΒΡ÷–ΒψOΈΣ‘≤–ΡΘ§OAΈΣΑκΨΕΒΡ‘≤ΫΜAC”ΎΒψDΘ§E «BCΒΡ÷–ΒψΘ§Ν§Ϋ”DEΘ§OEΘ°
(1)≈–ΕœDE”κΓ―OΒΡΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
(2)«σ÷ΛΘΚBC2ΘΫ2CDOEΘΜ
(3)»τ![]() Θ§«σOEΒΡ≥ΛΘ°
Θ§«σOEΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–ΘΈΣΝΥΝΥΫβ―ß…ζΦ“≥ΛΕ‘ΚΔΉ” Ι”Ο ÷ΜζΒΡΧ§Ε»«ιΩωΘ§ΥφΜζ≥ι»Γ≤ΩΖ÷―ß…ζΦ“≥ΛΫχ––Έ ΨμΒς≤ιΘ§ΖΔ≥ωΈ Ψμ150ΖίΘ§ΟΩΈΜ―ß…ζΦ“≥Λ1ΖίΘ§ΟΩΖίΈ ΨμΫω±μΟς“Μ÷÷Χ§Ε»Θ§ΫΪΜΊ ’ΒΡΈ ΨμΫχ––’ϊάμΘ®ΦΌ…ηΜΊ ’ΒΡΈ ΨμΕΦ”––ßΘ©Θ§≤ΔΜφ÷ΤΝΥ»γΆΦΥυ ΨΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ° ΗυΨί“‘…œ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©ΜΊ ’ΒΡΈ Ψμ ΐΈΣΖίΘ§ΓΑ―œΦ”Η……φΓ±≤ΩΖ÷Ε‘”Π…»–ΈΒΡ‘≤–ΡΫ«Ε» ΐΘΜ
Θ®2Θ©Α―Χθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©»τΫΪΓΑ¥”ά¥≤ΜΙήΓ±ΚΆΓΑ…‘Φ”―·Έ Γ± ”ΈΣΓΑΙήάμ≤Μ―œΓ±Θ§“―÷Σ»Ϊ–ΘΙ≤1200Οϊ―ß…ζΘ§«κΙάΦΤΗΟ–ΘΕ‘ΚΔΉ” Ι”Ο ÷ΜζΓΑΙήάμ≤Μ―œΓ±ΒΡΦ“≥Λ”–Εύ…Ό»ΥΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΒψAΘ®2Θ§aΘ©ΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψ «BΘ®bΘ§©¹3Θ©Θ§‘ρabΒΡ÷Β « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com