
 如图:已知DE∥BC,AD=1,DB=2,DE=3,则BC=________,△ADE和△ABC的面积之比为________.
如图:已知DE∥BC,AD=1,DB=2,DE=3,则BC=________,△ADE和△ABC的面积之比为________. =
= =
= ,三角形的面积公式为:
,三角形的面积公式为: ×高×底,可直接求出二者的比值.
×高×底,可直接求出二者的比值. =
= ,即:
,即: =
= =
= ,
, =
=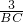 =
=
 h2
h2 ×h1×DE):(
×h1×DE):( ×h2×BC)=
×h2×BC)= =
= =1:9
=1:9

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
 16、如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论:
16、如图,已知DE∥BC,AB∥CD,E为AB的中点,∠A=∠B.下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整.
(1)如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com