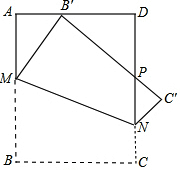
解:Ⅰ、过点N作NR⊥AB,垂足为R,连接BB′交MN于点Q.
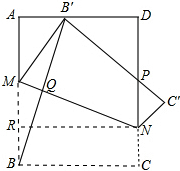
则由折叠知,△MBQ与△MB′Q关于直线MN对称,
∴MQ⊥BB′.
在△RNM和△ABB′中,∠A=∠MRN=90°,
∠ABB′+∠BMQ=∠RNM+∠BMN=90°
∴∠ABB′=∠RNM,
又∵RN=AB=1,
∴△RNM≌△ABB′,
∴BB′=MN.
Ⅱ、由Ⅰ可知△MQB∽△B′AB,
∵
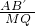
=

=
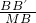
,
∵AB′=x,
则BB′=

,BQ=


,代入上式得:
BM=

(x
2+1).
Ⅲ、由Ⅱ得:BM=

(x
2+1),
CN=BR=BM-MR=

(x
2+1)-x=

(x-1)
2,
∵MB′∥NC′,
∴四边形MNC′B′是梯形,
∴S=

[

(x-1)
2+

(x
2+1)]×1=

(x
2-x+1),
由S=

(x
2-x+1)=

(x-

)
2+

,
故当x=

时,即B落在AD的中点处时,梯形面积最小,其最小值为

.
分析:Ⅰ、根据折叠的性质可知,∠A=∠MRN=90°,又∵∠ABB′=∠RNM,RN=AB=1,可知△ABB′≌△RNM,继而可知BB′=MN;
Ⅱ、由Ⅰ可知△MQB∽△B′AB,根据相似三角形的性质得到求y与x的函数关系式;
Ⅲ、由Ⅱ可得到MB′和CN的表达式,继而根据梯形的面积公式求出S的表达式,利用二次函数求出S的最小值.
点评:此题考查了翻折变换,要注意翻折不变性和正方形的性质等隐含条件.题目还涉及二次函数的最值问题,综合性较强.

 则由折叠知,△MBQ与△MB′Q关于直线MN对称,
则由折叠知,△MBQ与△MB′Q关于直线MN对称,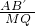 =
= =
=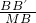 ,
, ,BQ=
,BQ=
 ,代入上式得:
,代入上式得: (x2+1).
(x2+1). (x2+1),
(x2+1), (x2+1)-x=
(x2+1)-x= (x-1)2,
(x-1)2, [
[ (x-1)2+
(x-1)2+ (x2+1)]×1=
(x2+1)]×1= (x2-x+1),
(x2-x+1), (x2-x+1)=
(x2-x+1)= (x-
(x- )2+
)2+ ,
, 时,即B落在AD的中点处时,梯形面积最小,其最小值为
时,即B落在AD的中点处时,梯形面积最小,其最小值为 .
.

 阅读快车系列答案
阅读快车系列答案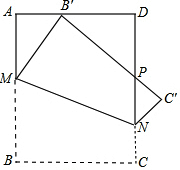
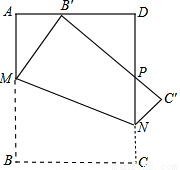
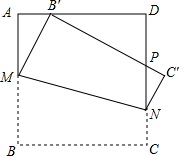 (2012•河东区二模)如图,将一个边长为1的正方形纸片ABCD折叠,使点B落在边AD上(不与A、D重合),MN为折痕,折叠后B′C′与DN交于P,则四边形MNC′B′面积最小值为
(2012•河东区二模)如图,将一个边长为1的正方形纸片ABCD折叠,使点B落在边AD上(不与A、D重合),MN为折痕,折叠后B′C′与DN交于P,则四边形MNC′B′面积最小值为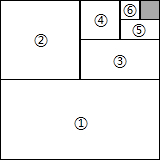 如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.
如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推. 的面积为
的面积为