
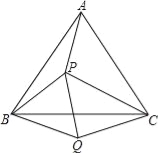
【题目】如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论错误的是( )
A.△BPQ是等边三角形
B.△PCQ是直角三角形
C.∠APB=150°
D.∠APC=135°
【答案】D
【解析】
试题分析:根据等边三角形性质得出∠ABC=60°,根据全等得出∠BPA=∠BQC,BP=BQ=4,QC=PA=3,∠ABP=∠QBC,求出∠PBQ=60°,即可判断A,根据勾股定理的逆定理即可判断B;求出∠BQP=60°,∠PQC=90°,即可判断C,求出∠APC+∠QPC=150°和PQ≠QC即可判断D.
∵△ABC是等边三角形, ∴∠ABC=60°, ∵△BQC≌△BPA,
∴∠BPA=∠BQC,BP=BQ=4,QC=PA=3,∠ABP=∠QBC,
∴∠PBQ=∠PBC+∠CBQ=∠PBC+∠ABP=∠ABC=60°,
∴△BPQ是等边三角形, ∴PQ=BP=4, ∵PQ2+QC2=42+32=25,PC2=52=25, ∴PQ2+QC2=PC2,
∴∠PQC=90°,即△PQC是直角三角形, ∵△BPQ是等边三角形, ∴∠BOQ=∠BQP=60°,
∴∠BPA=∠BQC=60°+90°=150°, ∴∠APC=360°﹣150°﹣60°﹣∠QPC=150°﹣∠QPC,
∵∠PQC=90°,PQ≠QC, ∴∠QPC≠45°,即∠APC≠135°, ∴选项A、B、C正确,选项D错误.


科目:初中数学 来源: 题型:
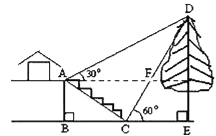
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆的半径等于5厘米,圆心到直线l的距离是:
(1)4厘米;(2)5厘米;(3)6厘米.
直线l和圆分别有几个公共点?分别说出直线l与圆的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下列各组线段为边,能组成三角形的是().
A. 2cm,3cm,5cmB. 5cm,6cm,10cm
C. 1cm,1cm,3cmD. 3cm,4cm,9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() 的边长
的边长![]() .某一时刻,动点
.某一时刻,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动;同时,动点
点匀速运动;同时,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动,问:
点匀速运动,问:

(1)经过多少时间,![]() 的面积等于矩形
的面积等于矩形![]() 面积的
面积的![]() ?
?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与![]() 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:
①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;
②三角形的三边a、b、c满足a2+c2=b2,则∠C=90°;
③△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④△ABC中,若 a:b:c=1:2:![]() ,则这个三角形是直角三角形.
,则这个三角形是直角三角形.
其中,假命题的个数为( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com