
阅读:如图,CE∥AB,

∴∠1=∠A,∠2=∠B.
∴∠ACD=∠1+∠2=∠A+∠B,这是一个有用的事实,请用这个事实,在如图5-102四边形ABCD内引一条和边平行的直线,求出∠A+∠B+∠C+∠D的度数.
科目:初中数学 来源: 题型:
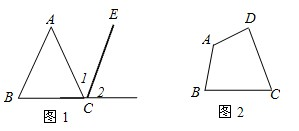
查看答案和解析>>
科目:初中数学 来源: 题型:
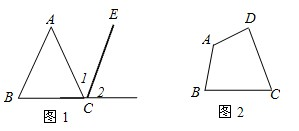
查看答案和解析>>
科目:初中数学 来源:2013届江苏省南京市鼓楼区中考二模数学试卷(带解析) 题型:解答题
阅读:
如图①,已知:正方形ABCD,面积为a,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接AG、BH、CE、DF,求四边形MNPQ的面积.


小明提出了如下的解决办法:如图②,分别将△AMH、△BNE、△CPF、△DQG分割并拼补成一个与正方形ABCD面积相等的新图形.
请你参考小明同学解决问题的方法,利用图形变换解决下列问题:
如图③,在正方形ABCD中,E1、E2、E3、E4分别为AB、BC、CA、DA的中点,P 1、P2, Q1、Q2,M 1、M2,N1、N2分别为AB、BC、CA、DA的三等分点.
(1)在图③中画出一个和正方形ABCD面积相等的新图形,并用阴影表示(保留画图痕迹);
(2)图③中四边形P4Q4M4N4的面积为 .
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省南京市鼓楼区中考二模数学试卷(解析版) 题型:解答题
阅读:
如图①,已知:正方形ABCD,面积为a,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接AG、BH、CE、DF,求四边形MNPQ的面积.

小明提出了如下的解决办法:如图②,分别将△AMH、△BNE、△CPF、△DQG分割并拼补成一个与正方形ABCD面积相等的新图形.
请你参考小明同学解决问题的方法,利用图形变换解决下列问题:
如图③,在正方形ABCD中,E1、E2、E3、E4分别为AB、BC、CA、DA的中点,P 1、P2, Q1、Q2,M 1、M2,N1、N2分别为AB、BC、CA、DA的三等分点.
(1)在图③中画出一个和正方形ABCD面积相等的新图形,并用阴影表示(保留画图痕迹);
(2)图③中四边形P4Q4M4N4的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com