分析:(1)利用积的乘方的性质,同底数幂相乘,底数不变指数相加进行计算即可得解;
(2)利用平方差公式与完全平方公式计算即可得解;
(3)根据任何非零数的零次幂等于1,有理数的负整数指数次幂等于正整数指数次幂的倒数计算即可得解;
(4)利用完全平方公式与多项式的乘法运算法则进行计算即可得解;
(5)把第二个方程整理为y=2x-8,然后利用代入消元法求解即可;
(6)根据y的系数互为相反数,利用加减消元法求解即可.
解答:解:(1)(-2a)
3-(-a)(3a)
2=-8a
3-(-a)(9a
2)
=-8a
3+9a
3=a
3;
(2)(a+3)(a
2-9)(a-3)
=(a
2-9)(a
2-9)
=a
4-18a
2+81;
(3)(-3)
0+(
-)
-2÷|-2|
=1+4÷2
=1+2
=3;
(4)(x+3)
2-(x-1)(x-2)
=x
2+6x+9-(x
2-3x+2)
=x
2+6x+9-x
2+3x-2
=9x+7;
(5)
,
由②得,y=2x-8③,
③代入①得,3x+2(2x-8)=5,
解得x=3,
把x=3代入③得,y=6-8=-2,
所以,方程组的解是
;
(6)
,
①+②得,4x+8=0,
解得x=-2,
把x=-2代入①得,-6-y+2=0,
解得y=-4,
所以,方程组的解是
.
点评:本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.















 )-2÷|-2|
)-2÷|-2|
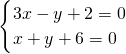 .
.