
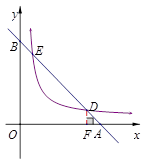
如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.
(1)若点D的坐标为(4,1),点E的坐标为(1,4):
① 分别求出直线l与双曲线的解析式;(3分)
② 若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?(4分)
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.(2分)
(1)①反比例函数的解析式为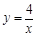 ,直线AB的解析式为y=-x+5;
,直线AB的解析式为y=-x+5;
②当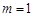 时,直线l与反比例函数有且只有一个交点;
时,直线l与反比例函数有且只有一个交点;
(2)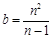
解析试题分析:(1)、①把点D或点E的坐标代入双曲线 (a≠0,x>0)中,易求反比例函数的解析式为
(a≠0,x>0)中,易求反比例函数的解析式为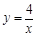 ,设直线AB的解析式为y=ax+b,再把点D或点E的坐标代入,可得一个二元一次方程组,求得直线AB的解析式为y = -x+5;
,设直线AB的解析式为y=ax+b,再把点D或点E的坐标代入,可得一个二元一次方程组,求得直线AB的解析式为y = -x+5;
② 依题意可设向下平移m(m>0)个单位后解析式为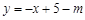 ,直线l与双曲线有且只有一个交点即
,直线l与双曲线有且只有一个交点即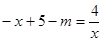 (整理得
(整理得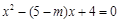 )的△=0即△=
)的△=0即△=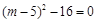 ,
,
解得: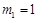 ,
,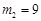 (舍去),即当
(舍去),即当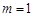 时,直线l与反比例函数有且只有一个交点;
时,直线l与反比例函数有且只有一个交点;
(2)、过点D作DF⊥OA于F(如下图),则△ADF∽△ABO得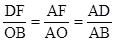 ,即
,即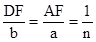 解得:DF=
解得:DF=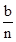 ,AF=
,AF=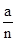 ;所以OF=OA-AF=a-
;所以OF=OA-AF=a-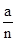 =
=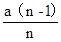 ,所以点D的坐标为(
,所以点D的坐标为(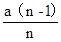 ,
,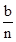 ),又因为点D在双曲线
),又因为点D在双曲线 (a≠0,x>0)上,所以
(a≠0,x>0)上,所以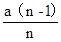 ×
×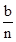 =a,所以
=a,所以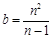 .
.
试题解析:(1) ①易求反比例函数的解析式为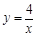 ,
,
直线AB的解析式为y = -x+5;(5分)
② 依题意可设向下平移m(m>0)个单位后解析式为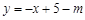 ,
,
由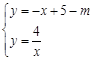 ,得
,得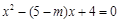 ,
,
∵ 平移后直线l与反比例函数有且只有一个交点,∴△=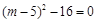 ,
,
∴ 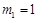 ,
,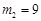 (舍去).
(舍去).
即当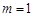 时,直线l与反比例函数有且只有一个交点;(5分)
时,直线l与反比例函数有且只有一个交点;(5分)
(2) 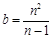 .(2分)
.(2分)
考点:1、用待定系数法求一次函数与反比例函数的解析式;2、一元二次方程;3、相似三角形.


科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xoy中,以点M(1,-1)为圆心,以 为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数
为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数 的图象经过点A、B、C,顶点为E.
的图象经过点A、B、C,顶点为E.
(1)求此二次函数的表达式;
(2)设∠DBC=a,∠CBE=b,求sin(a-b)的值;
(3)坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似.若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在边长为6的菱形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N.
(1)如图1,当点M在AB边上时,连接BN
①试说明: ;
;
②若∠ABC=60°,AM=4,求点M到AD的距离.
(2)如图2,若∠ABC=90°,记点M运动所经过的路程为x(6≤x≤12).试问:x为何值时,△ADN为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当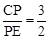 ,BP′=
,BP′= 时,求线段AB的长.
时,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在△ABC中,∠ACB=90°,∠A<45°,点O为AB中点,一个足够大的三角板的直角顶点与点O重合,一边OE经过点C,另一边OD与AC交于点M.
(1)如图1,当∠A=30°时,求证:MC2=AM2+BC2;
(2)如图2,当∠A≠30°时,(1)中的结论是否成立?如果成立,请说明理由;如果不成立,请写出你认为正确的结论,并说明理由;
(3)将三角形ODE绕点O旋转,若直线OD与直线AC相交于点M,直线OE与直线BC相交于点N,连接MN,则MN2=AM2+BN2成立吗?
答: (填“成立”或“不成立”)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q;
(i)当点P与A,B两点不重合时,求 的值;
的值;
(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年四川南充8分)如图,等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为BC边上一点(不与B,C重合),过点P作∠APE=∠B,PE交CD 于E.
(1)求证:△APB∽△PEC;
(2)若CE=3,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com