
(1)已知正方形ABCD ,点E、F、G、H分别在边AB、BC、CD、DA上,若EG⊥FH,求证EG = FH”(如图1);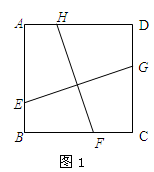
(2)如果把条件中的“正方形”改为“长方形”,并设AB =2,BC =3(如图2),试探究EG、FH之间有怎样的数量关系,并证明你的结论;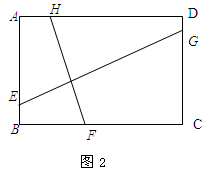
(3)如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”,并假设正方形ABCD的边长为1,FH的长为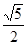 (如图3),试求EG的长度。
(如图3),试求EG的长度。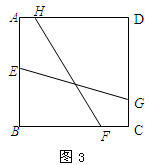
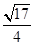
解析试题分析:因为ABCD是正方形,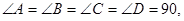
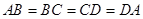
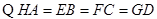
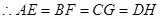

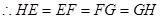
在(2)的条件下,此时仍然满足EG = FH”
过A作AM//EG,作AN//FH,连接MN,延长CB至P,使PB=DM,连接AP,过A作MN的垂线交MN于Q。
显然三角形ABP与ADM全等,AP=AM,角DAM=角BAP
可知角PAN=45°,三角形ANP与ANM全等,MN=NP=BN+DM
设DM=x
则:MC=1-x
AN=FH=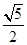
BN=1/2
MN=NP=BN+DM=1/2+x
NC=1-1/2=1/2
在直角三角形CMN中,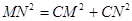
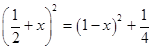
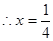
EG=AM=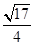
考点:相似三角形的判定
点评:解答本题的的关键是熟练掌握有两组角对应相等的两个三角形相似;两组边对应成比例且夹角相等的三角形相似.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
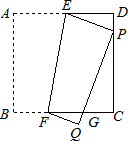 与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•金东区一模)如图,已知正方形ABCD的边长为8,以AB为直径的⊙O交对角线AC于点F,点E在⊙O上(E,F分别在直径AB的两侧).
(2012•金东区一模)如图,已知正方形ABCD的边长为8,以AB为直径的⊙O交对角线AC于点F,点E在⊙O上(E,F分别在直径AB的两侧).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com