
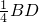 时,求∠ADC的大小.
时,求∠ADC的大小.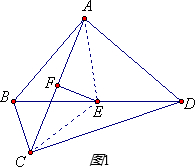 解:(1)如图,EF垂直平分AC.理由如下:
解:(1)如图,EF垂直平分AC.理由如下: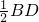 ,
,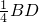 ,AE=CE=
,AE=CE=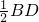 ,
,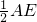 .
.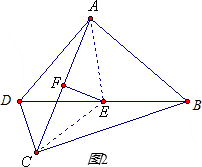 EF⊥AC,∠ECA=∠EAC=30°,
EF⊥AC,∠ECA=∠EAC=30°,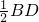 ,
,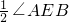 ,
,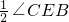 ,
,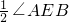 +
+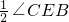 =
=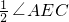 =60°;
=60°;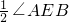 +
+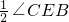 =
=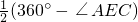 =120°.
=120°.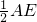 ,推出∠ECA=∠EAC=30°,根据三角形外角性质和等腰三角形性质求出∠ADE=
,推出∠ECA=∠EAC=30°,根据三角形外角性质和等腰三角形性质求出∠ADE=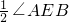 ,∠CDE=
,∠CDE=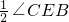 ,代入求出即可.
,代入求出即可.

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com