
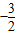 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由.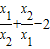 的值为整数的实数k的整数值.
的值为整数的实数k的整数值.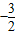 ,即2(x1+x2)2-9x1x2=-1.5,根据一元二次方程根与系数的关系求得方程两根的和与两根的积代入即可得到关于k的方程,即可求得k的值,然后判断是否满足即可;
,即2(x1+x2)2-9x1x2=-1.5,根据一元二次方程根与系数的关系求得方程两根的和与两根的积代入即可得到关于k的方程,即可求得k的值,然后判断是否满足即可;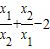 =4-
=4-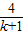 ,根据
,根据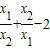 的值为整数,以及k的范围即可确定k的取值.
的值为整数,以及k的范围即可确定k的取值.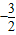 得
得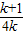 =-1.5
=-1.5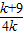 =-1.5的解.
=-1.5的解.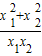 -2=
-2=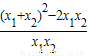 -2=
-2=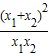 -4=
-4=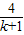 -4,
-4,

科目:初中数学 来源:2002年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《反比例函数》(01)(解析版) 题型:选择题
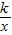 的图象过点(-2,3),那么下列各点在函数y=kx-2的图象上的是( )
的图象过点(-2,3),那么下列各点在函数y=kx-2的图象上的是( ) ,-1)
,-1) ,-11)
,-11)查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《一次函数》(01)(解析版) 题型:选择题
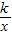 的图象过点(-2,3),那么下列各点在函数y=kx-2的图象上的是( )
的图象过点(-2,3),那么下列各点在函数y=kx-2的图象上的是( ) ,-1)
,-1) ,-11)
,-11)查看答案和解析>>
科目:初中数学 来源:2002年四川省中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2002年四川省中考数学试卷(解析版) 题型:选择题
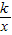 的图象过点(-2,3),那么下列各点在函数y=kx-2的图象上的是( )
的图象过点(-2,3),那么下列各点在函数y=kx-2的图象上的是( ) ,-1)
,-1) ,-11)
,-11)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com