(1)证明:连接OE,
∵BD=BF,
∴∠BDF=∠F,
∵OD=OE,
∴∠BDF=∠OED,
∴∠ODE=∠F,
∴OE∥BC,
∵在Rt△ABC中,∠ACB=90°,
∴∠OEA=90°,
即OE⊥AC,
∴AC是⊙O的切线;
(2)设半径为x,
∵OE∥BC,
∴△AOE∽△ABC,
∴
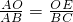
,
∵BC=6,AD=4,
∴AO=4+x,AB=4+2x,
∴
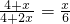
,
解得:x=4或x=-3(舍去).
∴⊙O的面积为:16π.
分析:(1)连接OE,由OD=OE,BD=BF,易证得∠OED=∠F,即可得OE∥BC,又由在Rt△ABC中,∠ACB=90°,即可得AC是⊙O的切线;
(2)首先设半径为x,易得△AOE∽△ABC,由相似三角形的对应边成比例,即可求得半径,继而求得答案.
点评:此题考查了切线的判定、相似三角形的判定与性质以及等腰三角形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

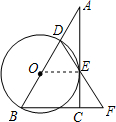
 在Rt△ABC中,∠ACB=90°,BD是⊙O的直径,弦DE与AC交于点E,且BD=BF.
在Rt△ABC中,∠ACB=90°,BD是⊙O的直径,弦DE与AC交于点E,且BD=BF. (1)证明:连接OE,
(1)证明:连接OE,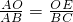 ,
,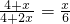 ,
,

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案