
 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )| A. | 88° | B. | 92° | C. | 106° | D. | 136° |
分析 首先根据∠BOD=88°,应用圆周角定理,求出∠BAD的度数多少;然后根据圆内接四边形的性质,可得∠BAD+∠BCD=180°,据此求出∠BCD的度数是多少即可.
解答 解:∵∠BOD=88°,
∴∠BAD=88°÷2=44°,
∵∠BAD+∠BCD=180°,
∴∠BCD=180°-44°=136°,
即∠BCD的度数是136°.
故选:D.
点评 (1)此题主要考查了圆内接四边形的性质和应用,要熟练掌握,解答此题的关键是要明确:①圆内接四边形的对角互补.②圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).
(2)此题还考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
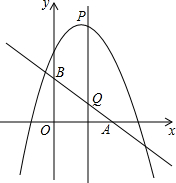 如图,已知直线y=-$\frac{3}{4}$x+3分别交x轴、y轴于点A、B,P是抛物线y=-$\frac{1}{2}$x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=-$\frac{3}{4}$x+3于点Q,则当PQ=BQ时,a的值是-1,4,4+2$\sqrt{5}$,4-2$\sqrt{5}$.
如图,已知直线y=-$\frac{3}{4}$x+3分别交x轴、y轴于点A、B,P是抛物线y=-$\frac{1}{2}$x2+2x+5的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=-$\frac{3}{4}$x+3于点Q,则当PQ=BQ时,a的值是-1,4,4+2$\sqrt{5}$,4-2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | B. | $\sqrt{12}÷\sqrt{3}$=2 | C. | ($\sqrt{5}$)-1=$\sqrt{5}$ | D. | ($\sqrt{3}$-1)2=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
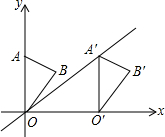 如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′是直线y=$\frac{4}{5}$x上一点,则点B与其对应点B′间的距离为5.
如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′是直线y=$\frac{4}{5}$x上一点,则点B与其对应点B′间的距离为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
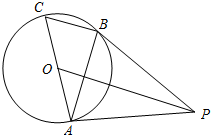 如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com