
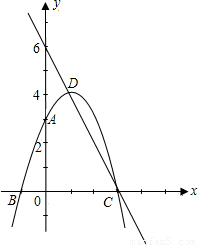
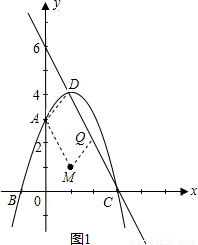
 НтЃКЃЈ1ЃЉЩшЙ§AЁЂBЁЂCШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊy=ax2+bx+cЃЌ
НтЃКЃЈ1ЃЉЩшЙ§AЁЂBЁЂCШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЮЊy=ax2+bx+cЃЌ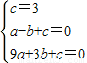 ЃЌ
ЃЌ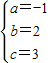 ЃЌ
ЃЌ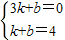 ЃЌ
ЃЌ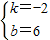 ЃЌ
ЃЌ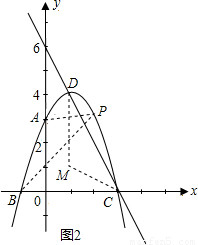
 ×3×2=3ЃЌ
×3×2=3ЃЌ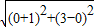 =
=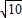 ЃЌ
ЃЌ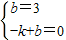 ЃЌ
ЃЌ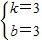 ЃЌ
ЃЌ AB•h=2ЃЌ
AB•h=2ЃЌ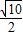 h=2ЃЌ
h=2ЃЌ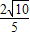 ЃЌ
ЃЌ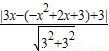 =
=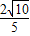 ЃЌ
ЃЌ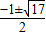 ЃЌ
ЃЌ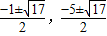 ЃЉ
ЃЉ

 Н№АцПЮЬУПЮЪБбЕСЗЯЕСаД№АИ
Н№АцПЮЬУПЮЪБбЕСЗЯЕСаД№АИ ЕЅдЊШЋФмСЗПМОэЯЕСаД№АИ
ЕЅдЊШЋФмСЗПМОэЯЕСаД№АИ аТЛЦИдБјЗЈУмОэЯЕСаД№АИ
аТЛЦИдБјЗЈУмОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 зјБъдЕуЃЎAЁЂBСНЕуЕФКсзјБъЗжБ№ЪЧЗНГЬx2-4x-12=0ЕФСНИљЃЌЧвcosЁЯDAB=
зјБъдЕуЃЎAЁЂBСНЕуЕФКсзјБъЗжБ№ЪЧЗНГЬx2-4x-12=0ЕФСНИљЃЌЧвcosЁЯDAB=
| ||
| 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 18ЁЂдкЦНУцжБНЧзјБъЯЕжаЃЌАбвЛИіЭМаЮЯШШЦзХдЕуЫГЪБеыа§зЊЕФНЧЖШЮЊІШЃЌдйвддЕуЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊkЕУЕНвЛИіаТЕФЭМаЮЃЌЮвУЧАбетИіЙ§ГЬМЧЮЊЁОІШЃЌkЁПБфЛЛЃЎР§ШчЃЌАбЭМжаЕФЁїABCЯШШЦзХдЕуOЫГЪБеыа§зЊЕФНЧЖШЮЊ90ЁуЃЌдйвддЕуЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊ2ЕУЕНвЛИіаТЕФЭМаЮЁїA1B1C1ЃЌПЩвдАбетИіЙ§ГЬМЧЮЊЁО90ЁуЃЌ2ЁПБфЛЛЃЎ
18ЁЂдкЦНУцжБНЧзјБъЯЕжаЃЌАбвЛИіЭМаЮЯШШЦзХдЕуЫГЪБеыа§зЊЕФНЧЖШЮЊІШЃЌдйвддЕуЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊkЕУЕНвЛИіаТЕФЭМаЮЃЌЮвУЧАбетИіЙ§ГЬМЧЮЊЁОІШЃЌkЁПБфЛЛЃЎР§ШчЃЌАбЭМжаЕФЁїABCЯШШЦзХдЕуOЫГЪБеыа§зЊЕФНЧЖШЮЊ90ЁуЃЌдйвддЕуЮЊЮЛЫЦжааФЃЌЯрЫЦБШЮЊ2ЕУЕНвЛИіаТЕФЭМаЮЁїA1B1C1ЃЌПЩвдАбетИіЙ§ГЬМЧЮЊЁО90ЁуЃЌ2ЁПБфЛЛЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com