Question

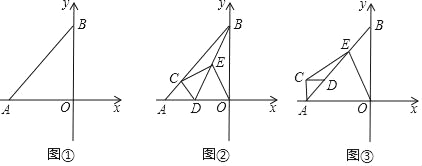
【题目】如图①，已知A（x，0）在x负半轴上，B（0，y）在y正半轴上，且x、y满足+y2﹣2my+m2=0，m＞0．

（1）判断△AOB的形状；

（2）如图②过OA上一点作CD⊥AB于C点，E是BD的中点，连接CE、OE，试判断CE与OE的数量关系与位置关系，并说明理由；（提示：可延长OE至F，使OE=EF，连接CF、DF、OC）

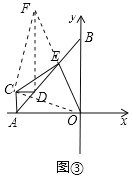
（3）将（2）中的△ACD绕A旋转至D落在AB上（如图③），其它条件不变，（2）中结论是否成立？请证明你的结论．

Answer 1

【答案】（1）△AOB是等腰直角三角形，理由详见解析；（2）CE=OE，CE⊥OE，理由详见解析；（3）（2）中的结论仍然成立，理由详见解析.

【解析】试题分析：（1）由算术平方根的性质和偶次方的非负性质求出x=m，y=m，得出OA=OB，即可得出结论；
（2）延长OE至F，使OE=EF，连接CF、DF、OC，由SAS证明△DEF≌△BEO，得出BO=DF，∠FDB=∠OBD，由SAS证明△OCA≌△FCD，得出OC=OF，∠OCA=∠FCD，进一步即可得出结论；
（3）延长OE至F，使OE=EF，连接CF、DF、OC，同（2）即可得出结论．

试题解析：(1)△AOB是等腰直角三角形，理由如下：

∵A(x,0)在x负半轴上,B(0,y)在y正半轴上,且x、y满足

x<0，y>0，

又

∴x+m=0，ym=0，

∴x=m，y=m，

∴OA=OB,

又

∴△AOB是等腰直角三角形；

(2)CE=OE，CE⊥OE.理由如下：

延长OE至F，使OE=EF，连接CF、DF、OC，如图②所示：

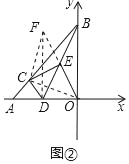
∵E是BD的中点，

∴DE=BE，

在△FDE和△OBE中,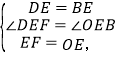

∴△DEF≌△BEO(SAS)，

∴BO=DF，∠FDB=∠OBD，

∴FD∥OB，

∴FD⊥AO，

∵∠BAO=CD⊥AB，

∴∠CDA==∠CAO=∠CDF，

∴CA=CD，

∵OA=OB，

∴OA=FD，

在△OCA和△FCD中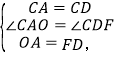

∴△OCA≌△FCD(SAS)，

∴OC=OF，∠OCA=∠FCD，

∴∠OCF=∠DCA=，

∴∠COF=，

又∵OE=EF，

∴∠OCE=∠OCF=,

∴∠COE=∠ECO=,∠CEO=，

∴CE=OE，CE⊥OE；

(3)(2)中的结论仍然成立.理由如下：

延长OE至F，使OE=EF，连接CF、DF、OC，如图③所示：

同(1)得：△DEF≌△BEO，

∴BO=DF，∠FDB=∠OBD

∴OA=FD,FD∥OB，

∴FD⊥AO，

∵∠BAO=,CD⊥AC,∠CDA==∠CAD，

∴∠CAO=∠DCA==∠FDC，CA=CD，

在△OCA和△FCD中,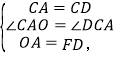

∴△OCA≌△FCD(SAS)，

∴OC=OF，∠OCA=∠FCD，

∴∠OCF=∠DCA=，

∴∠COF=，

又∵OE=EF，

∴∠OCE=∠OCF=

∴∠COE=∠ECO=,∠CEO=，

∴CE=OE，CE⊥OE；