
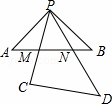
如图,将足够大的等腰直角三角板PCD的锐角顶点P放在另一个等腰直角三角板PAB的直角顶点处,三角板PCD绕点P在平面内转动,且∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N,设AB=2,AN=x,BM=y,则能反映y与x的函数关系的图象大致是( )
|
| A. |
| B. |
| C. |
| D. |
|
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=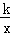 的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .
的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
有2条生产线计划在一个月(30天)内组装520台产品(每天产品的产量相同),按原先的组装速度,不能完成任务;若加班生产,每条生产线每天多组装2台产品,能提前完成任务.
(1)每条生产线原先每天最多能组装多少台产品?
(2)要按计划完成任务,策略一:增添1条生产线,共要多投资19000元;策略二:按每天能组装最多台数加班生产,每条生产线每天共要多花费350元;选哪一个策略较省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件是必然事件的是( )
|
| A. | 如果|a|=|b|,那么a=b |
|
| B. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 |
|
| C. | 半径分别为3和5的两圆相外切,则两圆的圆心距为8 |
|
| D. | 三角形的内角和是360° |
查看答案和解析>>
科目:初中数学 来源: 题型:
近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.
(1)求每台A种、B种设备各多少万元?
(2)根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系x Oy中(O为坐标原点),已知抛物线y=x2+bx+c过点A(4,0),B(1,﹣3).
Oy中(O为坐标原点),已知抛物线y=x2+bx+c过点A(4,0),B(1,﹣3).
(1)求b,c的值,并写出该抛物线的对称轴和顶点坐标;
(2)设抛物线的对称轴为直线l,点P(m,n)是抛物线上在第一象限的点,点E与点P关于直线l对称,点E与点F关于y轴对称,若四边形OAPF的面积为48,求点P的坐标;
(3)在(2)的条件下,设M是直线l上任意一点,试判断MP+MA是否存在最小值?若存在,求出这个最小值及相应的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com