
如图,在平面直角坐标系中,直线AB分别与x轴,y轴相交于A,B两点,OA,OB的长分别是方程x2﹣14x+48=0的两根,且OA<OB.
(1)求点A,B的坐标.
(2)过点A作直线AC交y轴于点C,∠1是直线AC与x轴相交所成的锐角,sin∠1= ,点D在线段CA的延长线上,且AD=AB,若反比例函数
,点D在线段CA的延长线上,且AD=AB,若反比例函数 的图象经过点D,求k的值.
的图象经过点D,求k的值.
(3)在(2)的条件下,点M在射线AD上,平面内是否存在点N,使以A,B,M,N为顶点的四边形是邻边之比为1:2的矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1)A(6,0),B(0,8)。
(2)k=84。
(3)存在。点N的坐标为(4,11)或(16,20)。
解析试题分析:(1)解一元二次方程,求得OA、OB的长度,得到点A、B的坐标。
解:解方程x2﹣14x+48=0,得:x1=6,x2=8。
∵OA,OB的长分别是方程x2﹣14x+48=0的两根,且OA<OB,∴OA=6,OB=8。
∴A(6,0),B(0,8)。
(2)如答图所示,作辅助线,构造全等三角形△AOB≌△DEA,求得点D的坐标;进而由题意,求出k的值。
如答图所示,过点D作DE⊥x轴于点E.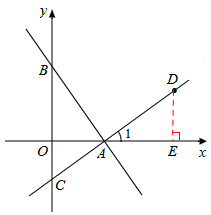
在Rt△AOB中,OA=6,OB=8,
由勾股定理得:AB=10。
∴ 。
。
∵sin∠1= ,∴∠OBA=∠1。
,∴∠OBA=∠1。
∵∠OBA+∠OAB=90°,∠1+∠ADE=90°,
∴∠OAB=∠ADE。
在△AOB与△DEA中,∵∠OBA=∠1,AB=AD,∠OAB=∠ADE,
∴△AOB≌△DEA(ASA)。∴AE=OB=8,DE=OA=6。∴OE=OA+AE=6+8=14。
∴D(14,6)。
∵反比例函数 的图象经过点D,∴k=14×6=84。
的图象经过点D,∴k=14×6=84。
(3)如答图所示,可能存在两种情形:
如图所示,若以A,B,M,N为顶点的四边形是邻边之比为1:2的矩形,
①当AB:AM1=2:1时,
过点M1作M1E⊥x轴于点E,
易证Rt△AEM1∽Rt△BOA,
∴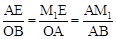 ,即
,即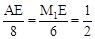
∴AE=4,M1E=3。
过点N1作N1F⊥y轴于点F,易证Rt△N1FB≌Rt△AEM1,
∴N1F=AE=4,BF=M1E=3,∴OF=OB+BF=8+3=11。
∴N1(4,11)。
②当AB:AM2=1:2时,同理可求得:N2(16,20)。
综上所述,存在满足条件的点N,点N的坐标为(4,11)或(16,20)。


科目:初中数学 来源: 题型:解答题
一次函数y=kx+4的图象经过点(-3,-2),则
(1)求这个函数表达式;并画出该函数的图象.
(2)判断(-5,3)是否在此函数的图象上;
(3)求把这条直线沿x轴向右平移1个单位长度后的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某社区活动中心为鼓励居民加强体育锻炼,准备购买10副某种品牌的羽毛球拍,每副球拍配x(x≥2)个羽毛球,供社区居民免费借用.该社区附近A、B两家超市都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均为30元,每个羽毛球的标价为3元,目前两家超市同时在做促销活动:
A超市:所有商品均打九折(按标价的90%)销售;
B超市:买一副羽毛球拍送2个羽毛球.
设在A超市购买羽毛球拍和羽毛球的费用为yA(元),在B超市购买羽毛球拍和羽毛球的费用为yB(元).请解答下列问题:
(1)分别写出yA、yB与x之间的关系式;
(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?
(3)若每副球拍配15个羽毛球,请你帮助该活动中心设计出最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知一次函数y=k1x+b(k1≠0)的图象分别与x轴,y轴交于A,B两点,且与反比例函数 (k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.
(k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.
(1)求一次函数的解析式;
(2)求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
| | 空调 | 彩电 |
| 进价(元/台) | 5400 | 3500 |
| 售价(元/台) | 6100 | 3900 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(3)在(2)的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低0.7万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
漳州三宝之一“水仙花”畅销全球,某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
| | A地 | B地 | C地 |
| 运费(元/件) | 20 | 10 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
抛物线 可以由抛物线
可以由抛物线 平移得到,则下列平移过程正确的是
平移得到,则下列平移过程正确的是
| A.先向左平移2个单位,再向上平移3个单位 |
| B.先向左平移2个单位,再向下平移3个位 |
| C.先向右平移2个单位,再向下平移3个单位 |
| D.先向右平移2个单位,再向上平移3个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com