
 解:过点A作关于y轴的对称点A',连接A'B,则A'B与y轴的交点即为点P的位置,
解:过点A作关于y轴的对称点A',连接A'B,则A'B与y轴的交点即为点P的位置,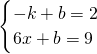 ,
,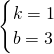 ,
,

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
 OB,OC的长分别是方程x2-4x+3=0的两根(OB<OC).
OB,OC的长分别是方程x2-4x+3=0的两根(OB<OC).查看答案和解析>>
科目:初中数学 来源: 题型:
 18、如果将点P绕定点M旋转180°后与点Q重合,那么点P与点Q关于点M对称,定点M叫对称中心,此时,点M是线段PQ的中点.如图,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0),点列P1、P2、P3、…中的相邻两点都关于△ABO的一个顶点对称,点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…,且这些对称中心依次循环,已知P1的坐标是(1,1),点P100的坐标为
18、如果将点P绕定点M旋转180°后与点Q重合,那么点P与点Q关于点M对称,定点M叫对称中心,此时,点M是线段PQ的中点.如图,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0),点列P1、P2、P3、…中的相邻两点都关于△ABO的一个顶点对称,点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…,且这些对称中心依次循环,已知P1的坐标是(1,1),点P100的坐标为查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•黄浦区二模)已知一次函数y=x+1的图象和二次函数y=x2+bx+c的图象都经过A、B两点,且点A在y轴上,B点的纵坐标为5.
(2012•黄浦区二模)已知一次函数y=x+1的图象和二次函数y=x2+bx+c的图象都经过A、B两点,且点A在y轴上,B点的纵坐标为5.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线y1与y2都与x轴交于点O(0,0)和点A,y1的顶点是B(2,-1),y2的顶点是C(2,-3),P是y1上的一个动点,过P作y轴的平行线交y2于点Q,分别过P,Q作x轴的平行线,分别交y1,y2于点P′,Q′,连接P′Q′.
如图,抛物线y1与y2都与x轴交于点O(0,0)和点A,y1的顶点是B(2,-1),y2的顶点是C(2,-3),P是y1上的一个动点,过P作y轴的平行线交y2于点Q,分别过P,Q作x轴的平行线,分别交y1,y2于点P′,Q′,连接P′Q′.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•恩施州)如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(2013•恩施州)如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com