
【题目】在①![]() ,②
,②![]() ,③
,③![]() 三对数值中,________是方程x+y=3的解,________是方程3x+2y=5的解,________是方程组
三对数值中,________是方程x+y=3的解,________是方程3x+2y=5的解,________是方程组![]() 的解.(填序号)
的解.(填序号)
【答案】①③ ②③ ③
【解析】
适合方程组的每一个方程的未知数的值即为方程组的一个解,只需把三个解观察代入方程,即可判断.
解: (1)将①![]() 代入方程x+y=3左边得:
代入方程x+y=3左边得: ![]() ,右边=3,
,右边=3,![]() 是方程x+y=3的解; 将②
是方程x+y=3的解; 将②![]() 代入方程x+y=3左边得:
代入方程x+y=3左边得:![]() ,右边=3,所以②
,右边=3,所以②![]() 不是x+y=3的解;将③
不是x+y=3的解;将③![]() 代入方程x+y=3左边得:
代入方程x+y=3左边得: ![]() ,右边=3,所以③
,右边=3,所以③![]() 是方程x+y=3的解;故答案为: ①③,
是方程x+y=3的解;故答案为: ①③,
(2)将①![]() 代入方程3x+2y=5左边得:
代入方程3x+2y=5左边得: ![]() ,右边=5,
,右边=5,![]() 不是方程3x+2y=5的解; 将②
不是方程3x+2y=5的解; 将②![]() 代入方程3x+2y=5左边得:
代入方程3x+2y=5左边得:![]() ,右边=5,所以②
,右边=5,所以②![]() 是3x+2y=5的解;将③
是3x+2y=5的解;将③![]() 代入方程3x+2y=5左边得:
代入方程3x+2y=5左边得: ![]() ,右边=5,所以③
,右边=5,所以③![]() 是方程3x+2y=5的解;故答案为: ②③,
是方程3x+2y=5的解;故答案为: ②③,
(3)根据(1)(2)可得③![]() 是x+y=3的解,也是方程3x+2y=5的解,故答案为: ③.
是x+y=3的解,也是方程3x+2y=5的解,故答案为: ③.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】计算
(1)﹣![]() ﹣[(﹣3) ﹣2×
﹣[(﹣3) ﹣2× ![]() ﹣8.5]÷(﹣
﹣8.5]÷(﹣ ![]() )
)
(2)![]() ×
×![]() ﹣0.25×(﹣4)×(﹣3);
﹣0.25×(﹣4)×(﹣3);
(3)(﹣1![]() )﹣1
)﹣1![]() +(﹣
+(﹣ ![]() )﹣3
)﹣3![]() ﹣(﹣1
﹣(﹣1![]() )
)
(4)![]() ÷4
÷4 ![]() ×(﹣
×(﹣![]() )+5﹣2×(﹣
)+5﹣2×(﹣ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班男、女同学分别参加植树活动,要求男、女同学各植8行树,男同学植的树比女同学植的树多,如果每行都比预定的多植一棵树,那么男、女同学植树的数目都超过100棵;如果每行都比预定的少植一棵树,那么男、女同学植树的数目都达不到100棵,这样原来预定男同学植树______棵,女同学植树______棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD. 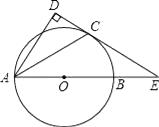
(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知CE⊥AB于点E,BD⊥AC于点D,BD与CE交于点O,且AO平分∠BAC.
(1)图中有多少对全等三角形?请你一一列举出来(不要求说明理由).
(2)小明说:欲说明BE=CD,可先说明△AOE≌△AOD得到AE=AD,再说明△ADB≌△AEC得到AB=AC,然后利用等式的性质即可得到BE=CD,请问他的说法正确吗?如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
(3)要得到BE=CD,你还有其他的思路吗?请仿照小明的说法具体说一说你的想法.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧 ![]() (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( ) 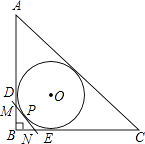
A.r
B.![]() ?r
?r
C.2r
D.![]() ?r
?r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,DE⊥BC,AB⊥BC,试说明:∠A=∠3.

解:因为DE⊥BC,AB⊥BC(已知),
所以∠DEC=∠ABC=90°(____________),
所以DE∥AB(____________________),
所以∠2=________(____________________),
∠1=________(____________________).
因为∠1=∠2(已知),
所以∠A=∠3(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的点,且CE=CF,点P、Q分别是AF、EF的中点,连接PD、PQ、DQ,则△PQD的形状是( )
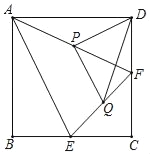
A. 等腰三角形 B. 直角三角形
C. 等腰非直角三角形 D. 等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com