

分析 (1)先根据勾股定理求出BE的长,进而可得出CE的长,求出E点坐标,再用勾股定理计算出OD即可;
(2)先判断出△APM∽△AED,表示出PM,再求出S四边形PMNE=-$\frac{1}{2}$(t-$\frac{5}{2}$)2+$\frac{25}{8}$确定出极值;
(3)分两种情况(Ⅰ)若以AE为等腰三角形的底,则ME=MA,利用中位线求出M点坐标,(Ⅱ)若以AE为等腰三角形的腰,则AM=AE=5,利用勾股定理和三角形相似求出即可.
解答 解:(1)依题意可知,折痕AD是四边形OAED的对称轴,
∴在Rt△ABE中,AE=AO=5,AB=4.
BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=3.
∴CE=2.
∴E点坐标为(2,4).
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD.
∴(4-OD)2+22=OD2.
解得:OD=$\frac{5}{2}$.
∴D点坐标为(0,$\frac{5}{2}$).
(2)∵PM∥ED,
∴△APM∽△AED.
∴$\frac{PM}{ED}=\frac{AP}{AE}$,
∵AP=t,ED=$\frac{5}{2}$,AE=5,
PM=$\frac{t}{5}$×$\frac{5}{2}$=$\frac{t}{2}$,
∵PE=5-t.
∵四边形PMNE为矩形.
S矩形PMNE=PM×PE=$\frac{t}{2}$×(5-t)=$\frac{1}{2}$t2+$\frac{5}{2}$t;
∴S四边形PMNE=-$\frac{1}{2}$(t-$\frac{5}{2}$)2+$\frac{25}{8}$.
∴当t=$\frac{5}{2}$时,S矩形PMNE有最大值$\frac{25}{8}$.
(3)(Ⅰ)若以AE为等腰三角形的底,则ME=MA(如图1)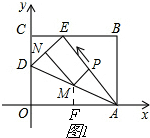
在Rt△AED中,ME=MA,
∵PM⊥AE,
∴P为AE的中点,
∴t=AP=$\frac{1}{2}$AE=$\frac{5}{2}$.
又∵PM∥ED,
∴M为AD的中点.
过点M作MF⊥OA,垂足为F,则MF是△OAD的中位线,
∴MF=$\frac{1}{2}$OD=$\frac{5}{4}$,OF=$\frac{1}{2}$OA=$\frac{5}{2}$,
∴当t=$\frac{5}{2}$时,(0<$\frac{5}{2}$<5),△AME为等腰三角形.
此时M点坐标为($\frac{5}{2}$,$\frac{5}{4}$).
(Ⅱ)若以AE为等腰三角形的腰,则AM=AE=5(如图1)
在Rt△AOD中,AD=$\sqrt{O{D}^{2}+A{O}^{2}}$=$\frac{5\sqrt{5}}{2}$.
过点M作MF⊥OA,垂足为F.
∵PM∥ED,
∴△APM∽△AED.
∴$\frac{AP}{AE}=\frac{AM}{AD}$
∴t=AP=$\frac{AM×AE}{AD}$=2$\sqrt{5}$,
∴PM=$\frac{1}{2}$t=$\sqrt{5}$.
∴MF=MP=$\sqrt{5}$,OF=OA-AF=OA-AP=5-2$\sqrt{5}$,
∴当t=2$\sqrt{5}$时,(0<2$\sqrt{5}$<5),此时M点坐标为(5-2$\sqrt{5}$,$\sqrt{5}$).
综合(Ⅰ)(Ⅱ)可知,t=$\frac{5}{2}$或t=2$\sqrt{5}$时,以A,M,E为顶点的三角形为等腰三角形,
相应M点的坐标为($\frac{5}{2}$,$\frac{5}{4}$)或(5-2$\sqrt{5}$,$\sqrt{5}$)
点评 此题是四边形综合题,主要考查了对折的性质,相似三角形的性质和判定,勾股定理,中位线,解本题的关键是表示出线段.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:填空题
| n(n是奇数,且n≥3) | 3 | 5 | 7 | 9 | … |
| m(m是偶数,且m≥4) | 4 | 12 | 24 | 40 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
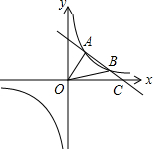 如图,已知A(a,a+1),B(a+3,a-1)是反比例函数y=$\frac{k}{x}$的图象上两点,必过A、B的直线y=mx+n交x轴于点C.
如图,已知A(a,a+1),B(a+3,a-1)是反比例函数y=$\frac{k}{x}$的图象上两点,必过A、B的直线y=mx+n交x轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
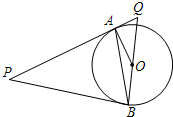 如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
如图所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
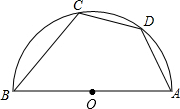 如图,AB是半圆的直径,∠ABC=50°,点D是$\widehat{AC}$的中点,则∠DAB等于( )
如图,AB是半圆的直径,∠ABC=50°,点D是$\widehat{AC}$的中点,则∠DAB等于( )| A. | 40° | B. | 50° | C. | 65° | D. | 70° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com