
����Ŀ����ͼ��Rt��OAB��ͼ��ʾ������ƽ��ֱ������ϵ�У�ֱ�DZ�OA��x���غϣ���OAB=90�㣬OA=4��AB=2����Rt��OAB�Ƶ�O��ʱ����ת90�㣬��B��ת����C��λ�ã�һ�����������þ�����O��C��A���㣮
��1����������ߵĽ���ʽ��
��2����x���Ϸ�������������һ����P������P��x���ƽ���߽��������ڵ�M���ֱ����P����M��x��Ĵ��ߣ���x����E��F���㣬�ʣ��ı���PEFM���ܳ��Ƿ������ֵ������У��������ֵ����д�������̣����û�У���˵�����ɣ�
��3�����x������һ����H�������������Ƿ���ڵ�N��ʹO��ԭ�㣩��C��H��N�ĵ㹹����OCΪһ�ߵ�ƽ���ı��Σ������ڣ����N������ꣻ�������ڣ���˵�����ɣ�

���𰸡�(1)��y=��x2+4x��(2)��10��(3)��N1��2+2![]() ����4����N2��2��2
����4����N2��2��2![]() ����4��
����4��
�����������������(1)��������ת�����ʿ����C�������A�����꣬����Ϊ�����߾���ԭ�㣬����y=ax2+bx�ѣ�2��4������4��0�����룬���a��b��ֵ��������������ߵĽ���ʽ��(2)���ı���PEFM���ܳ������ֵ�����P������ΪP��a����a2+4a�����������ߵĶԳ���֪OE=AF������EF=PM=4��2a��PE=MF=��a2+4a�������PEFM���ܳ�L=2[4��2a+����a2+4a��]=��2��a��1��2+10�����ú��������ʼ�������ı���PEFM���ܳ������ֵ��(3)�����������ϴ��ڵ�N��ʹO��ԭ�㣩��C��H��N�ĵ㹹����OCΪһ�ߵ�ƽ���ı��Σ��ɣ�1������������ߵĶ������꣬����C��x���ƽ���ߣ���x��û���������㣬��y=��4��x���ƽ���ߣ������������������㣬����������Ϊ�����N��������������x2+4x=��4���ⷽ�̼�������������꣮
���������(1)����ΪOA=4��AB=2������AOB�Ƶ�O��ʱ����ת90����
����ȷ����C������Ϊ��2��4������ͼ��֪��A������Ϊ��4��0����
����Ϊ�����߾���ԭ�㣬����y=ax2+bx�ѣ�2��4������4��0�����룬��![]() �����
�����![]()
���������ߵĽ���ʽΪy=��x2+4x��
(2)���ı���PEFM���ܳ������ֵ���������£�
�����⣬��ͼ��ʾ�����P������ΪP��a����a2+4a�����������ߵĶԳ���֪OE=AF��
��EF=PM=4��2a��PE=MF=��a2+4a��
�����PEFM���ܳ�L=2[4��2a+����a2+4a��]=��2��a��1��2+10��
����a=1ʱ������PEFM���ܳ������ֵ��Lmax=10��
(3)�����������ϴ��ڵ�N��ʹO��ԭ�㣩��C��H��N�ĵ㹹����OCΪһ�ߵ�ƽ���ı��Σ��������£�
��y=��x2+4x=����x��2��2+4��֪�������꣨2��4����
��֪��C�������Ƕ������֪꣬��C�㵽x��ľ���Ϊ4����λ���ȣ�
����C��x���ƽ���ߣ���x��û���������㣬��y=��4��x���ƽ���ߣ������������������㣬
���������������N��������������x2+4x=��4 ���x1=2+![]() ��x2=2��
��x2=2��![]()
��N������ΪN1��2+![]() ����4����N2��2��
����4����N2��2��![]() ����4����
����4����



 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڿμ��У�СӢ��С����С���ڲٳ��ϻ���A��B��������һ����Ͷ����Ϸ��ɳ������A�������÷�ֵ������B�������÷�ֵ��ͬ����ÿ�˸�Ͷɳ���Ĵ�ʱ���������Ĵ��ܷ���ͼ��ʾ��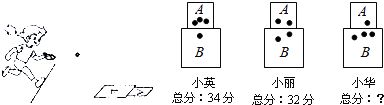
��1��ɳ������A�����B�������÷�ֵ�ֱ��Ƕ��٣�
��2�����С�����Ĵ��ܷ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ����Ϊ��ɽ���̡�ˮ���壬ij������ʵʩ��̬�����̣���չ��ҵ��ҵ��ȷ����2021��ʵ��ȫ��ɭ�ָ����ʴﵽ72.6%��Ŀ�꣮��֪����2019��ȫ��ɭ�ָ�����Ϊ60%�����2019�������ɭ�ָ�������ƽ��������Ϊx����x��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������Ϊ1�ġ�ABC��ν������²�������һ�β������ֱ��ӳ�AB��BC��CA����A1 �� B1 �� C1 �� ʹ��A1B=2AB��B1C=2BC��C1A=2CA��˳������A1 �� B1 �� C1 �� �õ���A1B1C1 �� �������ΪS1���ڶ��β������ֱ��ӳ�A1B1 �� B1C1 �� C1A1����A2 �� B2 �� C2 �� ʹ��A2B1=2A1B1 �� B2C1=2B1C1 �� C2A1=2C1A1 �� ˳������A2 �� B2 �� C2 �� �õ���A2B2C2 �� �������ΪS2 �� ��S2����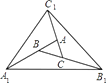
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��� ![]() ����������ȵ�ʵ������
����������ȵ�ʵ������
��1����m��ȡֵ��Χ��
��2����mΪ������ʱ���̵ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1�����㣺 ![]()
��2������a2��3������a3��2+2a5����a��
��3��(2a+b)(2a��b)+3(2a��b) 2+(��3a)(4a��3b)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BDƽ�֡�ABC����F��AB�ϣ���G��AC�ϣ�����FG��FC��FC��BD�ཻ�ڵ�H�������GFH���BHC��������֤����1=��2��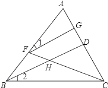
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������1��2��3��4������2017���г�����ͼ��ʾ��һ��������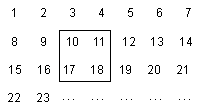
��1����һ�������ڱ��������ס4��������������С������Ϊ ![]() �����������ú�
�����������ú� ![]() ��ʽ�ӱ�ʾ�������Ӵ�С������ �� �� ��
��ʽ�ӱ�ʾ�������Ӵ�С������ �� �� ��
��2��������ס��4����֮�͵���416ʱ�� ![]() ��ֵ�Ƕ��٣�
��ֵ�Ƕ��٣�
��3������ס��4����֮���ܷ����622������ܣ��������ʱ ![]() ��ֵ��������ܣ���˵������.
��ֵ��������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y1=-x2+4x��ֱ��y2=2x������Լ������x��ȡһֵʱ��x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2����y1=y2����M=y1=y2�������жϣ��ٵ�x��2ʱ��M=y2���ڵ�x��0ʱ��xֵԽ��MֵԽ��ʹ��M����4��xֵ�����ڣ�����M=2����x=1��������ȷ���У�������
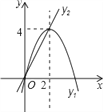
A. �ۢ� B. �ڢ� C. �ڢ� D. �٢�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com