
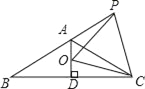
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F. 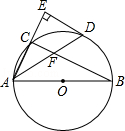
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
【答案】
(1)解:ED与⊙O的位置关系是相切.理由如下:
连接OD,
∵∠CAB的平分线交⊙O于点D,
∴ ![]() =
= ![]() ,
,
∴OD⊥BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
即BC⊥AC,
∵DE⊥AC,
∴DE∥BC,
∴OD⊥DE,
∴ED与⊙O的位置关系是相切
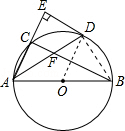
(2)解:连接BD.
∵AB是直径,
∴∠ADB=90°,
在直角△ABD中,BD= ![]() =
= ![]() =
= ![]() ,
,
∵AB为直径,
∴∠ACB=∠ADB=90°,
又∵∠AFC=∠BFD,
∴∠FBD=∠CAD=∠BAD
∴△FBD∽△BAD,
∴ ![]() =
= ![]()
∴FD= ![]()
∴AF=AD﹣FD=5﹣ ![]() =
= ![]() .
.

【解析】(1)连接OD,根据∠CAB的平分线交⊙O于点D,则 ![]() =
= ![]() ,依据垂径定理可以得到:OD⊥BC,然后根据直径的定义,可以得到OD∥AE,从而证得:DE⊥OD,则DE是圆的切线;(2)首先证明△FBD∽△BAD,依据相似三角形的对应边的比相等,即可求DF的长,继而求得答案.
,依据垂径定理可以得到:OD⊥BC,然后根据直径的定义,可以得到OD∥AE,从而证得:DE⊥OD,则DE是圆的切线;(2)首先证明△FBD∽△BAD,依据相似三角形的对应边的比相等,即可求DF的长,继而求得答案.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
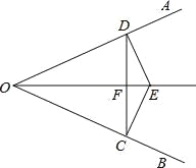
【题目】如图,已知:E 是∠AOB 的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接 CD,且交 OE 于点F.
(1)求证:OD=OC;
(2)求证:OE 是 CD 的垂直平分线;
(3)若∠AOB=60°,请你探究 OE,EF 之间有什么数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图所示,O是直线AB上一点,∠AOC=![]() ∠BOC,OC是∠AOD的平分线.
∠BOC,OC是∠AOD的平分线.

(1)求∠COD的度数.
(2)判断OD与AB的位置关系,并说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
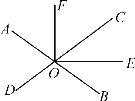
【题目】如图,直线AB,CD相交于点O,OE是∠COB的平分线,∠FOE=90°,若∠AOD=70°.
(1)求∠BOE的度数;
(2)OF是∠AOC的平分线吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】概念学习
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
从三角形![]() 不是等腰三角形
不是等腰三角形![]() 一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
理解概念
![]() 如图1,在
如图1,在![]() 中,
中,![]() ,
,![]() ,请写出图中两对“等角三角形”
,请写出图中两对“等角三角形”![]() 概念应用
概念应用
![]() 如图2,在
如图2,在![]() 中,CD为角平分线,
中,CD为角平分线,![]() ,
,![]() .
.
求证:CD为![]() 的等角分割线.
的等角分割线.
![]() 在
在![]() 中,
中,![]() ,CD是
,CD是![]() 的等角分割线,直接写出
的等角分割线,直接写出![]() 的度数.
的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com