
·ÖÎö £¨1£©ÏÈËă³ư·¨£¬ÔÙËă¼Ó·¨¼´¿É£»
£¨2£©ÏÈËăÀ¨ºÅÀïĂæµÄ£¬ÔÙ´Ó×óµ½Ó̉̉À´Î¼ÆËă¼´¿É£»
£¨3£©¸ù¾Ư³Ë·¨µÄ·ÖÅäÂɽøĐĐ¼ÆËă¼´¿É£»
£¨4£©¸ù¾Ư³Ë·¨µÄ·ÖÅäÂɵÄÄæÔËËă½øĐĐ¼ÆËă¼´¿É£»
£¨5£©ÏÈËă³Ë·½£¬ÔÙËă³Ë³ư£¬×îºóËă¼Ó¼ơ¼´¿É£®
½â´đ ½â£º£¨1£©-82+72¡Â36=-82+2
=-80£»
£¨2£©2$\frac{1}{2}$¡Á$\frac{1}{4}$¡Â£¨-9+19£©=$\frac{5}{2}$¡Á$\frac{1}{4}$¡Á$\frac{1}{10}$
=$\frac{1}{16}$£»
£¨3£©£¨$\frac{1}{2}$-$\frac{5}{9}$+$\frac{7}{12}$£©¡Á£¨-36£©=-18+20-21
=-19£»
£¨4£©1$\frac{1}{2}$¡Á$\frac{5}{7}$-£¨-$\frac{5}{7}$£©¡Á2$\frac{1}{2}$+£¨-$\frac{1}{2}$£©¡Â1$\frac{2}{5}$=$\frac{5}{7}$¡Á£¨$\frac{5}{2}$+$\frac{5}{2}$-$\frac{1}{2}$£©
=$\frac{5}{7}$¡Á$\frac{11}{2}$
=$\frac{55}{14}$£»
£¨5£©-13-£¨1-0.5£©¡Á$\frac{1}{3}$¡Á[2-£¨-3£©2]=-1-$\frac{1}{2}$¡Á$\frac{1}{3}$¡Á£¨-7£©
=-1+$\frac{7}{6}$
=$\frac{1}{6}$£®
µăÆÀ ±¾̀⿼²éÁËÓĐÀíÊưµÄ»́ºÏÔËËă£¬ƠÆÎƠÔËËă·¨ỘÊǽầâµÄ¹Ø¼ü£®



| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
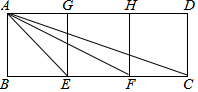 Èçͼ£¬ËıßĐÎABEG¡¢GEFH¡¢HFCD¶¼ÊDZ߳¤Îª1µÄƠư·½ĐΣ®
Èçͼ£¬ËıßĐÎABEG¡¢GEFH¡¢HFCD¶¼ÊDZ߳¤Îª1µÄƠư·½ĐΣ®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 2 | B£® | 3 | C£® | -$\frac{2}{3}$ | D£® | $\frac{2}{3}$ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 1 | B£® | 2 | C£® | 3 | D£® | 4 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com