(2009•怀柔区一模)把直线y=-2x+2沿x轴翻折恰好与抛物线y=ax2+bx+2交于点C(1,0)和点A(8,m).
(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,设点P是x轴上的任意一点(点P与点C不重合),若S△ABC=S△ACP,求满足条件的P点的坐标;
(3)设点P是x轴上的任意一点,试判断:PA+PB与AC+BC的大小关系,并说明理由.
【答案】
分析:(1)将直线y=-2x+2沿x轴翻折,那么新直线的斜率与原直线的斜率正好互为相反数,根据得出的直线的解析式可求得A点的坐标,然后将A、C的坐标代入抛物线中即可求得二次函数的解析式.
(2)先求出三角形ABC的面积,然后根据三角形ABC和三角形APC的面积相等,求出PC的长,即可求出P点的坐标.
(3)本题要分情况讨论:
①当P、C重合时,PA+PB=AC+BC;
②当P、C不重合时,可找出B点关于x轴的对称点(其实此点就是直线AC与y轴的交点)E,然后连接AE,此时发现AE正好过C点,因此AC+BC=AE,连接PB、PE,那么PA+PB=PA+PE,在三角形PAE中,根据三角形三边关系可得出PA+PE>PE,因此PA+PB>AC+BC.
综上所述即可得出所求的结论(主要根据轴对称和两点之间线段最短来求解).
解答:解:(1)依题意,直线y=-2x+2沿x轴翻折所得到的解析式为y=2x-2
又∵直线y=2x-2过点A(8,m),
∴m=14.即点A(8,14),
又抛物线y=ax
2+bx+2过点C(1,0)和点A(8,14),
a+b+2=0,64a+8b+2=14,
∴a=

,b=

,
∴抛物线的解析式为y=

x
2-

x+2.

(2)如图1,设点P坐标为(x,0),
则S
△ACP=

•PC•12=

|x-1|•14,
又∵S
△ABC=S
梯形ABOF-S
△BOC-S
△ACF=

(2+14)•8-

•1•2-

•7•14
=14.
∵S
△ABC=S
△ACP,
∴

|x-1|•14=14
∴x
1=3,x
2=-1,
∴点P坐标为(3,0)或(-1,0).
(3)如图2,结论:PA+PB≥AC+BC.
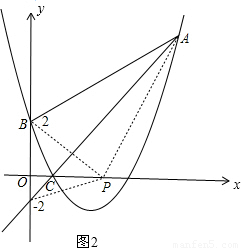
理由是:①当点P与点E重合时,有PA+PB=AC+BC.
②当点P异于点C时,
∵直线AC的解析式为y=2x-2,
∴直线AC与y轴相交于点E(0,-2).
则点E(0,-2)与B(0,2)关于x轴对称,
∴BC=EC,连接PE,则PE=PB.
∴AC+BC=AC+EC=AE,
∵在△APE中,有PA+PE>AE,
∴PA+PB=PA+PE>AE=AC+BC.
综上所得AP+BP≥AC+BC.
点评:本题考查了二次函数解析式的确定、图形面积的求法、轴对称图形等知识点.

 ,b=
,b= ,
, x2-
x2- x+2.
x+2.
 •PC•12=
•PC•12= |x-1|•14,
|x-1|•14, (2+14)•8-
(2+14)•8- •1•2-
•1•2- •7•14
•7•14 |x-1|•14=14
|x-1|•14=14


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案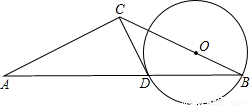
 ,BC=
,BC= ,求线段CP长的最大值.
,求线段CP长的最大值.