解:(1)2a
5•(-a)
2-(-a
2)
3•(-7a)
=2a
5•a
2+a
6•(-7a)
=2a
7-7a
7
=-5a
7;
(2)(4x
2y+5xy-7x)-(5x
2y+4xy+x)
=4x
2y+5xy-7x-5x
2y-4xy-x
=-x
2y+xy-8x;
(3)(

x
2y-2xy+y
2)•3xy
=

x
3y
2-6x
2y
2+3xy
3;
(4)(4x
3y-6x
2y
2+12xy
3)÷(2xy)
=2x
2-3xy+6y
2;
(5)[(4a+3b)(4a-3b)-(2a-5b)(8a+5b)]÷(-2b)
=[16a
2-9b
2-(16a
2+10ab-40ab-25b
2)]÷(-2b)
=(16a
2-9b
2-16a
2-10ab+40ab+25b
2)÷(-2b)
=(16b
2+30ab)÷(-2b)
=-8b-15a,
∵25a
2-10a+1+|4b+1|=0,即(5a-1)
2+|4b+1|=0,
∴5a-1=0且4b+1=0,
∴a=

,b=-

,
当a=

,b=-

时,原式=-8×(-

)-15×

=2-3=-1.
分析:(1)原式中两项分别利用积的乘方运算法则计算,再利用同底数幂的乘法法则计算,合并后即可得到结果;
(2)利用去括号法则去括号后,合并同类项即可得到结果;
(3)利用单项式乘以多项式的法则计算,即可得到结果;
(4)利用多项式除以单项式的法则计算,即可得到结果;
(5)将原式中括号中的第一项利用平方差公式化简,第二项利用多项式乘以多项式的法则计算,去括号合并后,再利用多项式除以单项式的法则计算,即可得到最简结果,然后将已知的等式左边前三项利用完全平方公式分解因式,利用两个非负数之和为0,两非负数同时为0转化为两个一元一次方程,求出方程的解得到a与b的值,将a与b的值代入化简后的式子中计算,即可得到原式的值.
点评:此题考查了整式的混合运算-化简求值,涉及的知识有:完全平方公式,平方差公式,多项式乘以多项式的法则,非负数的性质,以及多项式除以单项式的法则,熟练掌握公式及法则是解本题的关键.

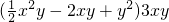
 x2y-2xy+y2)•3xy
x2y-2xy+y2)•3xy x3y2-6x2y2+3xy3;
x3y2-6x2y2+3xy3; ,b=-
,b=- ,
, ,b=-
,b=- 时,原式=-8×(-
时,原式=-8×(- )-15×
)-15× =2-3=-1.
=2-3=-1.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案