
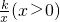 的图象上两点,AC⊥x轴,BD⊥y轴,垂足分别为C、D,AC、BD相交于点E,连接AB,CD.
的图象上两点,AC⊥x轴,BD⊥y轴,垂足分别为C、D,AC、BD相交于点E,连接AB,CD.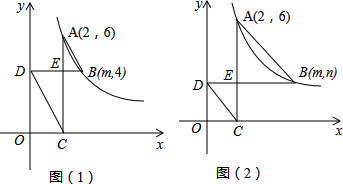
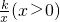 上的动点,且m>2,其余条件不变.
上的动点,且m>2,其余条件不变.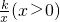 的图象上的点,
的图象上的点, ,
, ,
,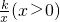 的图象上的点,
的图象上的点, ,
, ;3;
;3;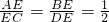 ,
,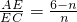 ,
,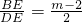 ,
, 上,
上, ,
,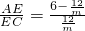 =
= ,
,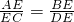 ,
,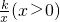 的图象上两点,首先将点A的坐标代入解析式,可求得反比例函数的表达式,再将B(m,4)代入,即可求得m的值;
的图象上两点,首先将点A的坐标代入解析式,可求得反比例函数的表达式,再将B(m,4)代入,即可求得m的值;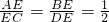 ,即可证得△AEB∽△CED,则可得∠EAB=∠ECD,继而证得AB∥CD;
,即可证得△AEB∽△CED,则可得∠EAB=∠ECD,继而证得AB∥CD;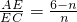 ,
,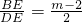 ,又由点B(m,n)在双曲线y=
,又由点B(m,n)在双曲线y= 上,可证得
上,可证得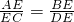 ,即可证得△AEB∽△CED,则可得∠EAB=∠ECD,继而证得AB∥CD;
,即可证得△AEB∽△CED,则可得∠EAB=∠ECD,继而证得AB∥CD;

科目:初中数学 来源: 题型:
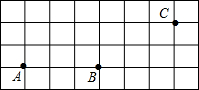 如图,线段AB、点C在正方形网格中,所有小正方形的边长都相等.
如图,线段AB、点C在正方形网格中,所有小正方形的边长都相等.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:
如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:查看答案和解析>>
科目:初中数学 来源: 题型:
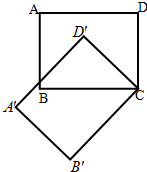 25、如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题:
25、如图,长方形ABCD绕点C按逆时针方向旋转45°后得到图形A'B'CD'.请回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com