
分析 首先把f(k)=$\frac{1}{(k+1)\sqrt{k}+k\sqrt{k+1}}$化简可得$\frac{1}{\sqrt{k}}$-$\frac{1}{\sqrt{k+1}}$,然后再代入k=1,k=2,k=3,…k=2011,即可得答案.
解答 解:f(k)=$\frac{1}{(k+1)\sqrt{k}+k\sqrt{k+1}}$
=$\frac{(k+1)\sqrt{k}-k\sqrt{k+1}}{[(k+1)\sqrt{k}]^{2}-(k\sqrt{k+1})^{2}}$
=$\frac{(k+1)\sqrt{k}-k\sqrt{k+1}}{k(k+1)^{2}-{k}^{2}(k+1)}$
=$\frac{(k+1)\sqrt{k}-k\sqrt{k+1}}{k(k+1)}$
=$\frac{1}{\sqrt{k}}$-$\frac{1}{\sqrt{k+1}}$,
f(1)+f(2)+f(3)+…+f(2011)
=$\frac{1}{\sqrt{1}}$-$\frac{1}{\sqrt{1+1}}$+$\frac{1}{\sqrt{2}}$-$\frac{1}{\sqrt{3}}$+$\frac{1}{\sqrt{3}}$-$\frac{1}{\sqrt{4}}$+…+$\frac{1}{\sqrt{2011}}$-$\frac{1}{\sqrt{2012}}$
=1-$\frac{1}{\sqrt{2012}}$
=$\frac{2012-\sqrt{2012}}{2012}$
=$\frac{1006-\sqrt{503}}{1006}$.
点评 此题主要考查了二次根式的化简计算,关键是熟练掌握利用平方差进行分母有理化的方法.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
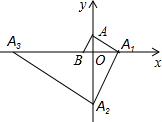 如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2015为止,则点A2015坐标为(-31008,0),.
如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2015为止,则点A2015坐标为(-31008,0),.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
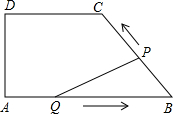 如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 10 | B. | -14 | C. | -12 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com