A
分析:由题意画出相应的图形,设出抛物线向上平移a个单位,且得到a大于1,利用平移规律“上加下减”表示出平移后抛物线的解析式,令解析式中y=0求出x的值,得到B和C的坐标,进而得到BC的长,由平移的距离AM=a,根据原抛物线的解析式求出M的坐标,确定出OM的长,可利用AM-OM表示出OA的长,又平移后抛物线的对称轴为y轴,得到O为BC的中点,再由三角形ABC为直角三角形,可得斜边上的中线AO等于斜边BC的一半,列出关于a的方程,求出方程的解可得到a的值,即为平移的距离.
解答:

解:设抛物线向上平移a(a>1)个单位,使抛物线与坐标轴有三个交点,
且这些交点能构成直角三角形,
则有平移后抛物线的解析式为:y=-2x
2-1+a,AM=a,
∵抛物线y=-2x
2-1与y轴的交点M为(0,-1),即OM=1,
∴OA=AM-OM=a-1,
令y=-2x
2-1+a中y=0,得到-2x
2-1+a=0,
解得:x=±
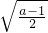
,
∴B(-
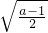
,0),C(
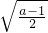
,0),即BC=2
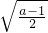
,
又△ABC为直角三角形,且B和C关于y轴对称,即O为BC的中点,
∴AO=

BC,即a-1=
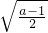
,
两边平方得:(a-1)
2=
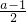
,
∵a-1≠0,∴a-1=

,
解得:a=

.
故选A
点评:此题考查了二次函数的图象及几何变换,涉及的知识有:平移规律,直角三角形的性质,抛物线与x轴的交点,利用了转化及数形结合的思想,解题的关键是根据题意表示出OA及BC,利用直角三角形斜边上的中线等于斜边的一半建立两边长的关系,借助方程来解决问题.

 个单位
个单位 个单位
个单位 个单位
个单位
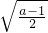 ,
,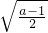 ,0),C(
,0),C(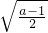 ,0),即BC=2
,0),即BC=2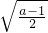 ,
, BC,即a-1=
BC,即a-1=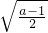 ,
,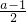 ,
, ,
, .
.
