
【题目】如图所示为圆柱形大型储油罐固定在U型槽上的横截面图.已知图中ABCD为等腰梯形(AB∥DC),支点A与B相距8 m,罐底最低点到地面CD距离为1 m.设油罐横截面圆心为O,半径为5 m,∠D=56°,求:U型槽的横截面(阴影部分)的面积.(参考数据:sin 53°≈0.8,tan 56°≈1.5,π≈3,结果保留整数)

【答案】U型槽的横截面积约为20 m2
【解析】
解:如图,连接AO、BO.过点A作AE⊥DC于点E,过点O作ON⊥DC于点N,ON交⊙O于点M,交AB于点F,则OF⊥AB.
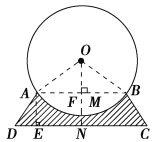
∵OA=OB=5 m,AB=8 m,
∴AF=BF=![]() AB=4(m),∠AOB=2∠AOF,
AB=4(m),∠AOB=2∠AOF,
在Rt△AOF中,sin∠AOF=![]() =0.8=sin 53°,
=0.8=sin 53°,
∴∠AOF=53°,则∠AOB=106°,
∵OF=![]() =3(m),由题意得:MN=1 m,
=3(m),由题意得:MN=1 m,
∴FN=OM-OF+MN=3(m),
∵四边形ABCD是等腰梯形,AE⊥DC,FN⊥AB,
∴AE=FN=3 m,DC=AB+2DE.
在Rt△ADE中,tan 56°=![]() =
=![]() ,
,
∴DE=2 m,DC=12 m.
∴S阴=S梯形ABCD-(S扇形OAB-S△OAB)=![]() (8+12)×3-
(8+12)×3-![]()
≈20(m2).
答:U型槽的横截面积约为20 m2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密).安全员是数学爱好者,制定加密规则为:明文x,y,z对应密文x+y+z,x-y+z,x-y-z.例如:明文1,2,3对应密文6,2,-4.当接收方收到密文12,4,-6时,则解密得到的明文为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环下去.
(1)填写下表:
剪的次数 | 1 | 2 | 3 | 4 | 5 |
正方形个数 | 4 | 7 | 10 |
|
|
(2)如果剪了8次,共剪出 个小正方形.
(3)如果剪n次,共剪出 个小正方形.
(4)设最初正方形纸片为1,则剪n次后,最小正方形的边长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
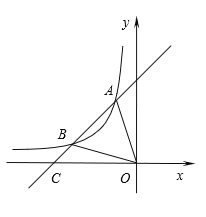
【题目】如图,一次函数y=x+4的图像与反比例函数![]() (k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
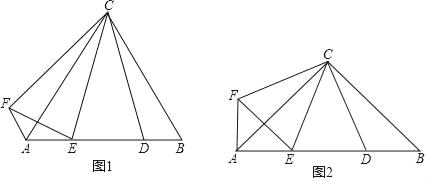
【题目】(1)操究发现:如图1,△ABC为等边三角形,点D为AB边上的一点,∠DCE=30°,∠DCF=60°且CF=CD
①求∠EAF的度数;
②DE与EF相等吗?请说明理由
(2)类比探究:如图2,△ABC为等腰直角三角形,∠ACB=90°,点D为AB边上的一点,∠DCE=45°,CF=CD,CF⊥CD,请直接写出下列结果:
①∠EAF的度数
②线段AE,ED,DB之间的数量关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道![]() 表示5与(-2)之差的绝对值,也可理解为5与-2两数在数轴上所对的两点之间的距离,试探索:
表示5与(-2)之差的绝对值,也可理解为5与-2两数在数轴上所对的两点之间的距离,试探索:
(1) 求![]() = ;
= ;
(2) 使得![]() =3成立的数是 ;
=3成立的数是 ;
(3) 由以上探索猜想,对于任何有理数x,则![]() 最小值是 ;
最小值是 ;
(4)由以上探索猜想,使得![]() 的成立的整数x是
的成立的整数x是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD边AB的中点,连接CE,过点B作BH⊥CE于F,交AC于G,交AD于H.下列说法: ![]() ;②点F是GB的中点;
;②点F是GB的中点; ![]() ;
; ![]() ,其中正确的结论的序号是_____________
,其中正确的结论的序号是_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y=-![]() x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
(1)当四边形OBCE是矩形时,求点C的坐标;
(2)如图②,若⊙C与y轴相切于点D,求⊙C的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com