
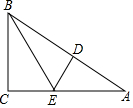
 如图,在Rt△ABC中,∠ACB=90°,两条直角边CB、CA的长度分别为6,8,折叠△ABC,使点A、B重合,DE为折痕,连接BE,则cos∠BEC=$\frac{7}{25}$.
如图,在Rt△ABC中,∠ACB=90°,两条直角边CB、CA的长度分别为6,8,折叠△ABC,使点A、B重合,DE为折痕,连接BE,则cos∠BEC=$\frac{7}{25}$. 分析 先根据图形翻折变换的性质得出BE=AE,设CE=x,则BE=AE=8-x,根据勾股定理求出x的值,再由锐角三角函数的定义即可得出结论.
解答 解:∵△BDE由△ADE翻折而成,
∴BE=AE.
设CE=x,则BE=AE=8-x,
在Rt△BCE中,BC2+CE2=BE2,即62+x2=(8-x)2,解得x=$\frac{7}{4}$,
∴CE=$\frac{7}{4}$,BE=$\frac{25}{4}$,
∴cos∠BEC=$\frac{CE}{BE}$=$\frac{\frac{7}{4}}{\frac{25}{4}}$=$\frac{7}{25}$.
故答案为$\frac{7}{25}$.
点评 本题考查的是翻折变换,熟知图形翻折不变性的性质是解答此题的关键.


科目:初中数学 来源: 题型:选择题
 如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.
如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2ab)•(-3ab)3=-54a4b4 | B. | 5x2•(3x3)2=15x12 | ||
| C. | (-0.1b)•(-10b2)3=-b7 | D. | (3×10n)($\frac{1}{3}$×10n)=102n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
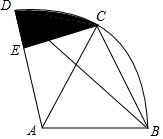 如图所示,在扇形BAD中,点C在$\widehat{BD}$上,且∠BDC=30°,AB=2$\sqrt{2}$,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )
如图所示,在扇形BAD中,点C在$\widehat{BD}$上,且∠BDC=30°,AB=2$\sqrt{2}$,∠BAD=105°,过点C作CE⊥AD,则图中阴影部分的面积为( )| A. | π-2 | B. | π-1 | C. | 2π-2 | D. | 2π+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com