
 已知a,b是正实数,
已知a,b是正实数,| a+b |
| 2 |
| ab |
| a |
| b |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a |
| b |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| a+b |
| 2 |
| ab |
| a |
| b |
| ab |
| ab |
| a+b |
| 2 |
| ab |
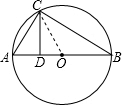 (2)如图,连接OC,
(2)如图,连接OC,| CD |
| AD |
| BD |
| CD |
| ab |
| a+b |
| 2 |
| a+b |
| 2 |
| ab |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
 (2012•资阳)已知a、b是正实数,那么,
(2012•资阳)已知a、b是正实数,那么,| a+b |
| 2 |
| ab |
| a |
| b |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a+b+c |
| 3 |
| 3 | abc |
| 3 | abc |
| a+b |
| 2 |
| ab |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川资阳卷)数学(带解析) 题型:解答题
已知a、b是正实数,那么,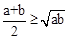 是恒成立的.
是恒成立的.
(1)(3分)由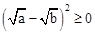 恒成立,说明
恒成立,说明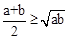 恒成立;
恒成立;
(2)(3分)填空:已知a、b、c是正实数,由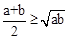 恒成立,猜测:
恒成立,猜测: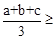 ▲ 也恒成立;
▲ 也恒成立;
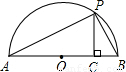
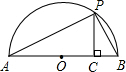
(3)(2分)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明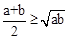 恒成立.
恒成立.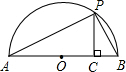
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川资阳卷)数学(解析版) 题型:解答题
已知a、b是正实数,那么,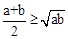 是恒成立的.
是恒成立的.
(1)(3分)由 恒成立,说明
恒成立,说明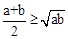 恒成立;
恒成立;
(2)(3分)填空:已知a、b、c是正实数,由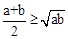 恒成立,猜测:
恒成立,猜测: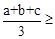 ▲ 也恒成立;
▲ 也恒成立;
(3)(2分)如图,已知AB是直径,点P是弧上异于点A和点B的一点,PC⊥AB,垂足为C,AC=a,BC=b,由此图说明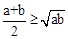 恒成立.
恒成立.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知a、b是正实数,那么,
已知a、b是正实数,那么, 是恒成立的.
是恒成立的.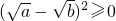 恒成立,说明
恒成立,说明 恒成立;
恒成立; 恒成立,猜测:
恒成立,猜测: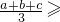 ______也恒成立;
______也恒成立; 恒成立.
恒成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com