
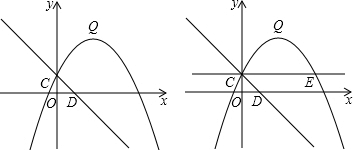
���� ��1���������ߵĽ���ʽΪy=a��x-2��2+3����C��0��1���������a��ֵ���ɣ�
��2����CΪֱ�Ƕ���ʱ����CM��CD��CM�����������M�������ֱ��CD�Ľ���ʽ��Ȼ�������ֱ��CM�Ľ���ʽ��Ȼ�����ֱ��CM�������ߵĽ������꼴�ɣ���DΪֱ�Ƕ���ʱ����DM��CD�������ֱ��MD�Ľ���ʽ��Ȼ��ֱ��CM�������ߵĽ������꼴�ɣ�
��3�����ڣ�����C����ֱ��QE�ĶԳƵ�C�䣬����C����x��ĶԳƵ�C�壬����C��C�壬��OD�ڵ�F����QE�ڵ�P�����PCF��Ϊ����������ܳ���С�������Σ�����ԳƵ����ʿ�֪����PCF���ܳ������߶�C��C��ij��ȣ�Ȼ�����C����C��N��y�ᣬȻ�����ݹ��ɶ��������C��C��ij����ɣ�
��� �⣺��1���������ߵĽ���ʽΪy=a��x-2��2+3��
��C��0��1������ã�4a+3=1����ã�a=-$\frac{1}{2}$��
��y=-$\frac{1}{2}$��x-2��2+3=-$\frac{1}{2}$x2+2x+1��
��2����CΪֱ�Ƕ���ʱ
��ͼ�٣���CM��CD��CM�����������M��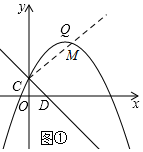
��ֱ��CDΪy=kx+1��
��OD=OC
��OD=1
��D��1��0��
��D��1��0������y=kx+1�ã�k=-1��
��y=-x+1��
��ֱ��CM�Ľ���ʽΪ��y=x+1����$\left\{\begin{array}{l}{y=x+1}\\{y=-\frac{1}{2}{x}^{2}+2x+1}\end{array}\right.$����֮�ã�M��2��3 ����ǡ����Q���غϣ�
��DΪֱ�Ƕ���ʱ����ͼ����ʾ��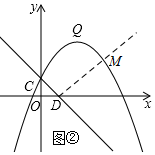
��ֱ��MD�Ľ���ʽΪy=x+b������D���������ã�1+b=0�����b=-1��
��MD�Ľ���ʽΪy=x-1��
��y=x-1��y=-$\frac{1}{2}$x2+2x+1������ã�x=$\sqrt{5}$+1��x=$\sqrt{5}$-1��
��M��$\sqrt{5}$+1��$\sqrt{5}$����1-$\sqrt{5}$��-$\sqrt{5}$����
�������������������M�����㣬�ֱ��ǣ�2��3 ��$\sqrt{5}$+1��$\sqrt{5}$����1-$\sqrt{5}$��-$\sqrt{5}$����
��3�����ڣ�
��ͼ����ʾ������C����ֱ��QE�ĶԳƵ�C�䣬����C����x��ĶԳƵ�C�壬����C��C�壬��OD�ڵ�F����QE�ڵ�P�����PCF��Ϊ����������ܳ���С�������Σ�����ԳƵ����ʿ�֪����PCF���ܳ������߶�C��C��ij��ȣ�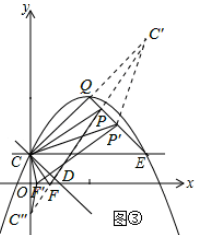
���߶�OD��ȡ���ڵ�F����һ��F�䣬���߶�QE��ȡ���ڵ�P����һ��P�䣬����F��C�壬F��P�䣬P��C�䣮
����ԳƵ����ʿ�֪����P��CF����ܳ�=F��C��+F��P��+P��C�䣮
��F��C��+F��P��+P��C���ǵ�C�䣬C��֮������߶Σ�
��F��C��+F��P��+P��C�䣾C��C�壬����P��CF����ܳ����ڡ�PCE���ܳ�����
���ͼ����ʾ������C��E��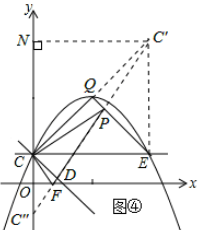
��C��C�����ֱ��QE�Գƣ���QCEΪ����ֱ�������Σ�
���QC��EΪ����ֱ�������Σ�
���CEC��Ϊ����ֱ�������Σ�
���C���������4��5����
��C��C�����x��Գƣ����C�������Ϊ��0��-1����
����C����C��N��y���ڵ�N����NC��=4��NC��=4+1+1=6��
��Rt��C��NC���У��ɹ��ɶ����ã�C��C��=$\sqrt{C��{N}^{2}+C��{N}^{2}}$=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$��
������������P���F���ƶ������У���PCF���ܳ�������Сֵ����СֵΪ2$\sqrt{13}$��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ���������Ľ���ʽ���������ֱ������ֱ�ߵ�һ����ϵ���˻�Ϊ-1�ǽ�����⣨2���Ĺؼ���������ԳƵ����ʽ������ε��ܳ�ת��Ϊ�߶�C��C��ij��ǽ�����⣨3���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
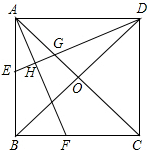 ��֪����ͼ����������ABCD�У�O�ǶԽ��ߵĽ��㣬AFƽ�֡�BAC��DH��AF�ڵ�H����AC�ڵ�G��DH�ӳ��߽�AB�ڵ�E��
��֪����ͼ����������ABCD�У�O�ǶԽ��ߵĽ��㣬AFƽ�֡�BAC��DH��AF�ڵ�H����AC�ڵ�G��DH�ӳ��߽�AB�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
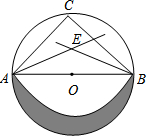 ��ͼ����O��ֱ��AB=2��C�ǻ�AB���е㣬AE��BE�ֱ�ƽ�֡�BAC�͡�ABC����EΪԲ�ģ�AEΪ�뾶������EAB����ȡ3������Ӱ���ֵ����Ϊ��������
��ͼ����O��ֱ��AB=2��C�ǻ�AB���е㣬AE��BE�ֱ�ƽ�֡�BAC�͡�ABC����EΪԲ�ģ�AEΪ�뾶������EAB����ȡ3������Ӱ���ֵ����Ϊ��������| A�� | $\frac{13}{4}$$\sqrt{2}$-4 | B�� | 7$\sqrt{2}$-4 | C�� | 6-$\frac{5}{4}$$\sqrt{2}$ | D�� | $\frac{{3\sqrt{2}-5}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪����y=kx+b��k��0����ͼ����ͼ����y=-2kx+b��k��0����ͼ������ǣ�������
��֪����y=kx+b��k��0����ͼ����ͼ����y=-2kx+b��k��0����ͼ������ǣ�������| A�� | 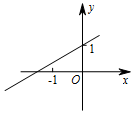 | B�� | 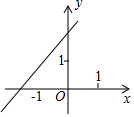 | C�� | 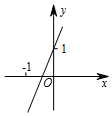 | D�� | 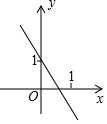 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
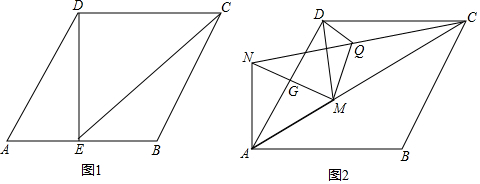
 ��ͼ����ֱ������ϵ�У���A�Ƿ���������y1=$\frac{k}{x}$ͼ����һ�㣬AB��x����������ڵ�B����C��OB���е㣬һ�κ���y2=ax+b��ͼ��A��C���㣬��y���ڵ�D��0��-2������AOB�����Ϊ4
��ͼ����ֱ������ϵ�У���A�Ƿ���������y1=$\frac{k}{x}$ͼ����һ�㣬AB��x����������ڵ�B����C��OB���е㣬һ�κ���y2=ax+b��ͼ��A��C���㣬��y���ڵ�D��0��-2������AOB�����Ϊ4�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD�У���ADC�Ľ�ƽ����DE���BCD�Ľ�ƽ����CA�ཻ��E�㣬DE��BC�ڵ�F������AF����֪��ACD=32�㣬��CDE=58�㣮
��ͼ���ı���ABCD�У���ADC�Ľ�ƽ����DE���BCD�Ľ�ƽ����CA�ཻ��E�㣬DE��BC�ڵ�F������AF����֪��ACD=32�㣬��CDE=58�㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com