
不解方程,判别下列方程的根的情况:
(1)2x2+3x-4=0;(2)16y2+9=24y;(3)5(x2+1)-7x=0.
|
(1)∵a=2,b=3,c=-4,∴b2-4ac-32-4×2×(-4)=41>0. ∴方程有两个不相等的实数根. (2)∵a=16,b=-24,c=9,∴b2-4ac=(-24)2-4×16×9=0. ∴方程有两个相等的实数解. (3)将原方程化为一般形式5x2-7x+5=0. ∵a=5,b=-7,c=5,∴b2-4ac=(-7)2-4×5×5=49-100=-51<0. ∵方程无实数解. |
|
分析:要判定上述方程的根的情况,只要看根的判别式Δ=b2-4ac的值的符号就可以了. 注意:对有些方程要先将其整理成一般形式,再正确确定a,b,c的符号. 方法提炼:确定a,b,c值时,先要将方程化为一般式,且不要把它们的符号弄错. |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3 |
| 2 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| b |
| a |
| c |
| a |
| b |
| 2a |
| b |
| a |
| b |
| 2a |
| c |
| a |
| b |
| 2a |
| b |
| 2a |
| b2-4ac |
| 4a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
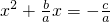
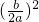 ,得
,得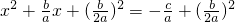 ,即
,即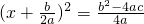
查看答案和解析>>
科目:初中数学 来源:《22.2 降次-解一元二次方程》2009年同步练习(2)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com