
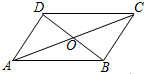
 如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC,AC=8,BD=6.
如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC,AC=8,BD=6.分析 (1)由已知条件易证△AOD≌△COB,由此可得OD=OB,进而可证明四边形ABCD是平行四边形;
(2)由(1)和已知条件可证明四边形ABCD是菱形,由菱形的面积公式即可得解.
解答 解:
(1)∵O是AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠ADO=∠CBO,
在△AOD和△COB中,
$\left\{\begin{array}{l}{∠ADO=∠CBO}\\{∠AOD=∠COB}\\{OA=OC}\end{array}\right.$,
∴△AOD≌△COB,
∴OD=OB,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,
∴?ABCD的面积=$\frac{1}{2}$AC•BD=24.
点评 此题主要考查平行四边形的判定和菱形的判断和性质.熟练掌握各种特殊四边形的性质定理和判定定理是解题的关键.


科目:初中数学 来源: 题型:填空题
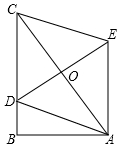 如图,在Rt△ABC中,∠B=90°,∠BAC=60°,AB=1,点D在BC边上,以AC为对角线的平行四边形ADCE中,当DE的长最小时,平行四边形ADCE的面积为$\frac{\sqrt{3}}{2}$.
如图,在Rt△ABC中,∠B=90°,∠BAC=60°,AB=1,点D在BC边上,以AC为对角线的平行四边形ADCE中,当DE的长最小时,平行四边形ADCE的面积为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
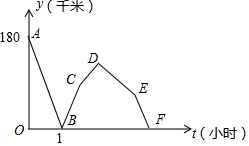 一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶,两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示,请结合图象提供的信息解答下列问题:
一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城后均停止行驶,两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示,请结合图象提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
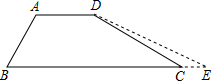 为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12$\sqrt{3}$米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=$\frac{3}{13}$$\sqrt{3}$,则CE的长为8米.
为加强防汛工作,某市对一拦水坝进行加固.如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12$\sqrt{3}$米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=$\frac{3}{13}$$\sqrt{3}$,则CE的长为8米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com