Question

19．已知：多项式$\frac{1}{4}{x^{n+1}}$-3x+1的次数是3．
（1）填空：n=2；
（2）直接判断：单项式$\frac{1}{2}{a^n}$b与单项式-3a²bⁿ是否为同类项否（填“是”或“否”）；
（3）如图，线段AB=12cm，点C是直线AB上一点，且BC=n•AC，若点D是AC的中点，求线段CD的长．

Answer 1

分析 （1）根据单项式的次数的概念列出关于n的方程，解方程即可；
（2）根据同类项的概念进行判断即可；
（2）分点C是线段AB上的点、点C是线段BA的延长线上的点两种情况，根据线段中点的定义、结合图形计算即可．

解答 解：（1）∵多项式$\frac{1}{4}{x^{n+1}}$-3x+1的次数是3，
∴n+1=3，
解得，n=2，
故答案为：2；
（2）单项式$\frac{1}{2}$a²b与单项式-3a²b²不是同类项，
故答案为：否；
（3）①显然，点C不在线段AB的延长线上，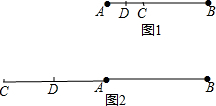
②如图1，当点C是线段AB上的点时
∵n=2，BC=n•AC
∴BC=2AC
∵AB=12，
∴AC=4，又∵D是AC的中点，
∴CD=2；
②如图2，当点C是线段BA的延长线上的点时，
∵n=2，BC=n•AC，
∴BC=2AC，
∵AB=12，
∴AC=12，
又∵D是AC的中点，
∴CD=6．
综上所述，CD=2或6．

点评 本题考查的是单项式的概念、同类项的概念以及两点间的距离的定义，所含字母相同，并且相同字母的指数也相同，这样的项叫做同类项．