
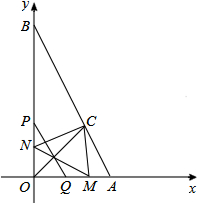
 ��ͼ����ƽ��ֱ������ϵ�У���A��2��0����B��0��4������AOB��ƽ���߽�AB�ڵ�C������P�ӵ�O��������ÿ��2����λ���ȵ��ٶȣ���y�����B�������˶���PQ��AB����x���ڵ�Q������P��Q������ֱ��OC�ĶԳƵ�M��N������MC��NC��MN�����P�˶���ʱ��Ϊt��0��t��2����
��ͼ����ƽ��ֱ������ϵ�У���A��2��0����B��0��4������AOB��ƽ���߽�AB�ڵ�C������P�ӵ�O��������ÿ��2����λ���ȵ��ٶȣ���y�����B�������˶���PQ��AB����x���ڵ�Q������P��Q������ֱ��OC�ĶԳƵ�M��N������MC��NC��MN�����P�˶���ʱ��Ϊt��0��t��2�������� ��1���������������ε����ʣ��ó�OP��OQ�Ĺ�ϵ�����M��N�����ꣻ
��2�����ͼ1���������ߣ��ɱ���ʽ�����C�����ꣻ
��3������������ϵʽΪ�ֶκ�������Ҫ�������ۣ���ͼ2-1����ͼ2-2��ʾ���˶��������ص����֣���Ӱ���ı仯���ֱ���⣻
�ڵ��غϲ��ֵ�������ڡ�CMN�����ʱ����MNC���OAB�ص�����ͼ�ε������OC�ֳ�1��2�����֣���OM��2ʱ����S��CNS=2S��CSDʱ��NS=2SD��
�õ�SM=2SN����D��MN���е㣬�����D���������ֱ��AB�Ľ���ʽ�����t��ֵ��
��� �⣺��1����PQ��AB��
��$\frac{OP}{OB}$=$\frac{OQ}{OA}$����$\frac{OP}{4}$=$\frac{OQ}{2}$��
��OP=2OQ��
��P��0��2t����
��Q��t��0����
�߶Գ���OCΪ��һ���Ľ�ƽ���ߣ�
��ԳƵ�����Ϊ��M��2t��0����N��0��t����
��2�����ͼ1������C��CF��x���ڵ�F��CE��y���ڵ�E��
�����⣬��֪�ı���OECFΪ�����Σ��������α߳�Ϊx��
����CE��x�ᣬ
��$\frac{BE}{OB}$=$\frac{CE}{OA}$����$\frac{4-x}{4}$=$\frac{x}{2}$����ã�x=$\frac{4}{3}$
��C��������$\frac{4}{3}$��$\frac{4}{3}$����
��PQ��AB��
��$\frac{OP}{OB}$=$\frac{OQ}{OA}$����$\frac{OP}{4}$=$\frac{OQ}{2}$��
��OP=2OQ��
��P��0��2t����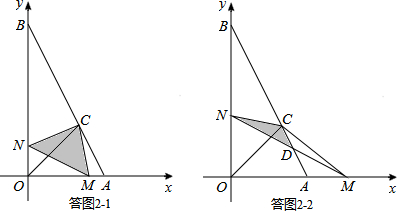
��Q��t��0����
�߶Գ���OCΪ��һ���Ľ�ƽ���ߣ�
��ԳƵ�����Ϊ��M��2t��0����N��0��t����
��3���ٵ�0��t��1ʱ�����ͼ2-1��ʾ����M���߶�OA�ϣ��ص��������ΪS��CMN��
S��CMN=S�ı���CMON-S��OMN
=��S��COM+S��CON��-S��OMN
=��$\frac{1}{2}$•2t��$\frac{4}{3}$+$\frac{1}{2}$•t��$\frac{4}{3}$��-$\frac{1}{2}$•2t•t
=-t2+2t��
��1��t��2ʱ�����ͼ2-2��ʾ����M��OA���ӳ����ϣ���MN��AB���ڵ�D�����ص��������ΪS��CDN��
��ֱ��MN�Ľ���ʽΪy=kx+b����M��2t��0����N��0��t�������$\left\{\begin{array}{l}{2tk+b=0}\\{b=t}\end{array}\right.$
���$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=t}\end{array}\right.$��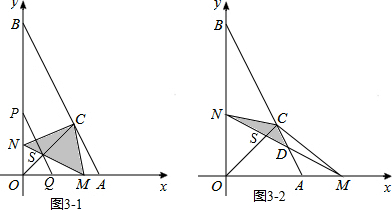
��y=-$\frac{1}{2}$x+t��
ͬ�����ֱ��AB�Ľ���ʽΪ��y=-2x+4��
����y=-$\frac{1}{2}$x+t��y=-2x+4����õ�D�ĺ�����Ϊ$\frac{8-2t}{3}$��
S��CDN=S��BDN-S��BCN
=$\frac{1}{2}$��4-t��•$\frac{8-2t}{3}$-$\frac{1}{2}$��4-t����$\frac{4}{3}$
=$\frac{1}{3}$t2-2t+$\frac{8}{3}$��
����������S=$\left\{\begin{array}{l}{{-t}^{2}+2t��0��t��1��}\\{{\frac{1}{3}t}^{2}-2t+\frac{8}{3}��1��t��2��}\end{array}\right.$��
�ڵ�0��t��1ʱ����t=$\frac{8}{5}$ʱ����MNC���OAB�ص�����ͼ�ε������OC�ֳ�1��2�����֣�
��ͼ3-1����0��t��1ʱ��
��S��CNS=$\frac{1}{2}$S��CSM����NS=$\frac{1}{2}$SM����S��OSN=$\frac{1}{2}$S��OSM=$\frac{1}{2}$S��OSQ��
��OQ=$\frac{1}{2}$OM��
�൱0��t��1ʱ��OM��2��
�൱0��t��1ʱ����MNC���OAB�ص�����ͼ�ε������OC�ֳ�1��2�����֣�
��ͼ3-2����S��CNS=2S��CSDʱ��NS=2SD��
��SM=2SN����ND=MD��
��D��t��$\frac{t}{2}$����
��ֱ��AB�Ľ���ʽΪy=-2x+4��
��$\frac{t}{2}$=-2t+4����t=$\frac{8}{5}$��
������������0��t��1ʱ����t=$\frac{8}{5}$ʱ����MNC���OAB�ص�����ͼ�ε������OC�ֳ�1��2�����֣�
���� ���⿼���˶��κ�����һ�κ���������ϵ���������ơ�ͼ��������㡢�������⺯��ͼ���֪ʶ�㣮�ѵ����ڵڣ�2���ʣ���ȷ�ؽ��з������ۣ��ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��OB�ǡ�AOC�Ľ�ƽ���ߣ�OD�ǡ�COE�Ľ�ƽ���ߣ������AOB=40�㣬��COE=60�㣬���BOD�Ķ���Ϊ���ٶȣ�
��ͼ��OB�ǡ�AOC�Ľ�ƽ���ߣ�OD�ǡ�COE�Ľ�ƽ���ߣ������AOB=40�㣬��COE=60�㣬���BOD�Ķ���Ϊ���ٶȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | k��4 | B�� | k��4 | C�� | k��4 | D�� | k��4��k��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��OA��OB��OD��OE�ֱ��ǡ�AOC����BOC��ƽ���ߣ����DOE=45�ȣ�
��ͼ��OA��OB��OD��OE�ֱ��ǡ�AOC����BOC��ƽ���ߣ����DOE=45�ȣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com