Question

6．在△ABC中，点D为△ABC的三条内角平分线的交点，BE⊥AD于点E，

（1）当∠BAC=80°，∠ACB=60°时，∠BDC=130°．∠DBE=30°．
（2）当∠BAC=α，∠ACB=β时，用含有α的代数式表示∠BDC的度数，用含有β的代数式表示∠DBE的度数．
（3）如图2，若AD平分∠BAC，CD和BD分别平分△ABC的外角∠CBM和∠BCN，BE⊥AD于点E，（2）中的两个结论是否发生变化？

Answer 1

分析 （1）根据三角形内角和定理以及角平分线的定义，可得∠ABD=20°，∠BAD=∠CAD=40°，∠ACD=30°，再根据∠BDC=∠BDE+∠CDE进行计算即可；
（2）根据三角形内角和定理以及角平分线的定义，求得∠DBC+∠DCB，在△BCD中，根据∠BDC=180°-（∠DBC+∠DCB）进行计算即可，根据BE⊥AD，可得∠DBE=90°-∠BDE，据此计算即可；
（3）根据三角形内角和定理以及角平分线的定义，即可得出若AD平分∠BAC，CD分别平分△ABC的外角∠CBM和∠BCN，BE⊥AD于点E，则（2）中的两个结论发生变化．

解答 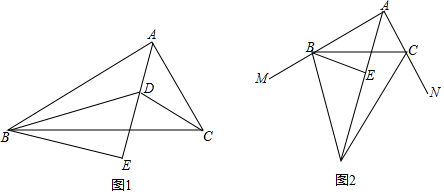解：（1）∵∠BAC=80°，∠ACB=60°，
∴∠ABC=40°，
∵点D为△ABC的三条内角平分线的交点，
∴∠ABD=20°，∠BAD=∠CAD=40°，∠ACD=30°，
∴∠BDC=∠BDE+∠CDE
=（∠ABD+∠BAD）+（∠ACD+∠CAD）
=（20°+40°）+（30°+40°）
=130°，
∵∠BDE=60°，BE⊥AD，
∴∠DBE=90°-60°=30°；
故答案为：130°，30°；

（2）∵∠BAC+∠CBA+∠ACB=180°，∠BAC=α
∴∠CBA+∠ACB=180°-∠BAC=180°-α
∵DB平分∠ABC，DC平分∠ACB，
∴∠DBC+∠DCB=$\frac{1}{2}$（∠CBA+∠ACB）=$\frac{1}{2}$（180°-α），
∴△BCD中，∠BDC=180°-（∠DBC+∠DCB）=180°-$\frac{1}{2}$（180°-α）=90°+$\frac{1}{2}$α；
∵∠BAC=α，∠ACB=β，
∴∠ABC=180°-α-β，
∵DB平分∠ABC，AD平分∠BAC，
∴∠ABD=$\frac{1}{2}$∠ABC=$\frac{1}{2}$（180°-α-β），∠BAD=$\frac{1}{2}$α，
∵∠BDE是△ABD的外角，
∴∠BDE=∠ABD+∠BAD=$\frac{1}{2}$（180°-α-β）+$\frac{1}{2}$α=90°-$\frac{1}{2}$β，
∵BE⊥AD，
∴∠DBE=90°-∠BDE=90°-（90°-$\frac{1}{2}$β）=$\frac{1}{2}$β；

（3）若AD平分∠BAC，CD分别平分△ABC的外角∠CBM和∠BCN，BE⊥AD于点E，则（2）中的两个结论发生变化．
理由：∵∠BAC+∠CBA+∠ACB=180°，∠BAC=α，
∴∠CBA+∠ACB=180°-∠BAC=180°-α，
∵∠MBC+∠ABC=180°，∠NCB+∠ACB=180°，
∴∠MBC+∠NGB=360°-∠ABC-∠ACB=360°-（180°-α）=180°+α，
∵BD，CD分别平分△ABC的外角∠CBM和∠BCN，
∴∠DBC=$\frac{1}{2}$∠MBC，∠DCB=$\frac{1}{2}$∠NCB，
∴∠DBC+∠DCB=$\frac{1}{2}$∠MBC+$\frac{1}{2}$∠NCB=$\frac{1}{2}$（180°+α）=90°+$\frac{1}{2}$α，
∵∠BDC+∠DBC+∠DCB=180°，
∴∠BDC=180°-（∠DBC+∠DCB）=180°-（90°+$\frac{1}{2}$α）=90°-$\frac{1}{2}$α，
∵∠BAC=α，∠ACB=β，
∵∠MBC是△ABC的外角，
∴∠MBC=α+β，
∵BD平分∠MBC，
∴∠MBD=$\frac{1}{2}$∠MBC=$\frac{1}{2}$（α+β），
∵∠MBD是△ABD的外角，AD平分∠BAC，
∴∠BAD=$\frac{1}{2}$α，∠MBD=∠BAD+∠ADB，
∵BE⊥AD，
∴Rt△BDE中，∠DBE=90°-∠ADB=90°-（∠MBD-∠BAD）
=90°-∠MBD+∠BAD
=90°-$\frac{1}{2}$（α+β）+$\frac{1}{2}$α
=90°-$\frac{1}{2}$β．
故结论发生变化．

点评 本题考查了三角形内角和定理，角平分线的定义，三角形外角的性质的综合应用．解题时注意：三角形的一个外角等于和它不相邻的两个内角的和；三角形内角和是180°．