
如图,AD∥BC,点E、F在BC上,∠1=∠2,AF⊥DE,垂足为点O.

(1)求证:四边形AEFD是菱形;
(2)若BE=EF=FC,求∠BAD+∠ADC的度数;
(3)若BE=EF=FC,设AB=m,CD=n,求四边形ABCD的面积.
|
(1) (4分)证明:(方法一)∵AF⊥DE∴∠1+∠3=90°即:∠3=90°-∠1 ∴∠2+∠4=90°即:∠4=90°-∠2 又∵∠1=∠2 ∴∠3=∠4 ∴AE=EF ∵AD∥BC ∴∠2=∠5 ∵∠1=∠2 ∴∠1=∠5 ∴AE=AD ∴EF=AD 2分 ∵AD∥EF ∴ 四边形AEFD是平行四边形 1分又∵AE=AD ∴ 四边形AEFD是菱形 1分( 方法二)∵AD∥BC ∴∠2=∠5∵∠1=∠2 ∴∠1=∠5 ∵AF⊥DE ∴∠AOE=∠AOD=90°
在 △AEO和△ADO中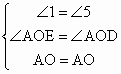 ∴△AEO ∴△AEO在△AEO和△FEO中 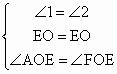 ∴△AEO ∴△AEO∴AF 与ED互相平分 1分∴四边形AEFD是平行四边形 又∵AF⊥DE ∴四边形AEFD是菱形 1分 (2)(5分)∵菱形AEFD ∴AD=EF ∵BE=EF ∴AD=BE 又∵AD∥BC ∴四边形ABED是平行四边形 1分 ∴AB∥DE ∴∠BAF=∠EOF 同理可知四边形AFCD是平行四边形
∴AF∥DC ∴∠EDC=∠EOF 又∵AF⊥ED ∴∠EOF=∠AOD=90° ∴∠BAF=∠EDC=∠EOF=90° 2分 ∴∠5+∠6=90° 1分 ∴∠BAD+∠ADC=∠BAF+∠6+∠5+∠EDC=270° 1分 (3)(3分)由(2)知∠BAF=90°平行四边形AFCD ∴AF=CD=n 又∵AB=m 由(2)知平行四边形ABED ∴DE=AB=m 由(1)知OD= |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com